Confidence Intervals using Profile Likelihood

Calculates confidence intervals for one or more parameters in a fitted model object. A function that returns the log-likelihood must be supplied, either directly via the argument loglik or using a logLikFn S3 generic.

Usage

profileCI(
  object,
  loglik,
  ...,
  parm = "all",
  level = 0.95,
  profile = TRUE,
  mult = 32,
  faster = TRUE,
  epsilon = -1,
  flat = 1e-06,
  lb,
  ub,
  optim_args = list()
)

Arguments

object

A fitted model object. This object must have a coef S3 method. If faster = TRUE then it must also have a vcov S3 method. If necessary, these may be created using .S3method(). For example, if object is a list inheriting from class "foo", with coefficients in object$coefficients and variance-covariance matrix in object$vcov, then use .S3method("coef", "foo", function(x) x$coefficients) and .S3method("vcov", "foo", function(x) x$vcov).

loglik

A named function that returns the log-likelihood based on input parameter values and data. The first argument must be the vector of model parameters. If the likelihood is zero for any observation in the data then the function should return -Inf.

Alternatively, loglik does not need to be supplied if a logLikFn S3 method has been created for object. The profileCI package provides logLikFn.glm, which is used in an example in Examples.

...

Further arguments to be passed to loglik.

parm

A vector specifying the parameters for which confidence intervals are calculated, either a vector of numbers or a vector of names. The default, which = "all", produces confidence intervals for all the parameters.

level

The confidence level required. A numeric scalar in (0, 1).

profile

A logical scalar. If TRUE then confidence intervals based on a profile log-likelihood are returned. If FALSE then intervals based on approximate large sample normal theory, which are symmetric about the MLE, are returned.

mult

A positive numeric scalar. Controls the increment by which the parameter of interest is increased/decreased when profiling above/below its MLE. The increment is mult * se / 100 where se is the estimated standard error of the estimator of the parameter. Decreasing mult profiles at more points but will be slower.

faster

A logical scalar. If faster = TRUE then the profiling of the log-likelihood is in search of a lower (upper) confidence limit is started at the corresponding symmetric lower (upper) confidence limit.

epsilon

Only relevant if profile = TRUE. A numeric vector of values that determine the accuracy of the confidence limits. epsilon is recycled to the length of the parameter vector parm.

If epsilon[i] > 0 then this value is passed as the argument epsilon to the itp::itp function, which estimates the parameter values for which the profile log-likelihood for parameter i drops to the value that defines the confidence limits, once profiling has been successful in finding an interval within which this value lies.
If epsilon[i] < 0 quadratic interpolation is used, which will tend to be faster.
If epsilon[i] = 0 then linear interpolation is used, which will be faster still.

flat

A positive numeric scalar used to avoid continuing a search for a confidence limits in cases where the profile log-likelihood becomes flat. If a reduction in profile log-likelihood is less than flat * mult / 100 then the search is stopped. The value of the returned confidence limit is Inf for an upper limit and -Inf for a lower limit.

lb, ub

Optional numeric vectors of length length(parm). If supplied, lb[i] and/or ub[i] place respective lower and upper bounds on the interval over which profiling takes place for parameter parm[i]. If a bound is reached before a confidence limit is determined or before the profile log-likelihood is determined to have become flat, then the relevant limit is returned as NA. Elementwise, lb must be smaller than, and ub larger than, coef(object).

optim_args

A list of further arguments (other than par and fn) to pass to stats::optim. For example, optim_args = list(method = "BFGS", control = list(trace = 1)) changes the method used from "Nelder-Mead" to "BFGS" and sets trace to provide the lowest level of tracing information.

Value

An object of class c("profileCI", "matrix", "array"). A numeric matrix with 2 columns giving the lower and upper confidence limits for each parameter. These columns are labelled as (1-level)/2 and 1-(1-level)/2, expressed as a percentage, by default 2.5% and 97.5%. The row names are the names of the parameters supplied in parm.

If profile = TRUE then the returned object has extra attributes crit, level and for_plot. The latter is a named list of length equal to the number of parameters. Each component is a 2-column numeric matrix. The first column contains values of the parameter and the second column the corresponding values of the profile log-likelihood. The profile log-likelihood is equal to the attribute crit at the limits of the confidence interval. The attribute level is the input argument level. If faster = FALSE or epsilon > 0 then the attributes lower_pars and upper_pars are lists that provide, for each profiling, the values of the parameters for the last maximisation of the log-likelihood.

A matrix with columns giving the object c("profileCI", "matrix", "array").

Details

The default, epsilon = -1, should work well enough in most circumstances, but to achieve a specific accuracy set epsilon to be a small positive value, for example, epsilon = 1e-4.

The defaults mult = 32 and faster = TRUE are designed to calculate confidence intervals fairly quickly. If the object returned from profileCI is plotted, using plot.profileCI, then we will not obtain a smooth plot of a profile log-likelihood. Setting faster = FALSE and reducing mult, perhaps to 8 or 16 should produce a smoother plot.

The arguments flat1, lb and ub are provided to prevent a call to profileCI hanging in a search for a confidence limit that will never be found.

Examples

## From example(glm)
counts <- c(18, 17, 15, 20, 10, 20, 25, 13, 12)
outcome <- gl(3, 1, 9)
treatment <- gl(3, 3)
glm.D93 <- glm(counts ~ outcome + treatment, family = poisson())
confint(glm.D93)
#> Waiting for profiling to be done...
#>                  2.5 %      97.5 %
#> (Intercept)  2.6958215  3.36655581
#> outcome2    -0.8577018 -0.06255840
#> outcome3    -0.6753696  0.08244089
#> treatment2  -0.3932548  0.39325483
#> treatment3  -0.3932548  0.39325483
confint.default(glm.D93)
#>                  2.5 %      97.5 %
#> (Intercept)  2.7095672  3.37947764
#> outcome2    -0.8505027 -0.05800787
#> outcome3    -0.6707552  0.08478093
#> treatment2  -0.3919928  0.39199279
#> treatment3  -0.3919928  0.39199279

# A Poisson log-linear GLM logLikFn.glm S3 method is provided in profileCI
# so we do not need to supply loglik explicitly
prof <- profileCI(glm.D93)
prof
#>                   2.5%       97.5%
#> (Intercept)  2.6958271  3.36656379
#> outcome2    -0.8576884 -0.06255514
#> outcome3    -0.6753594  0.08244109
#> treatment2  -0.3932489  0.39324886
#> treatment3  -0.3932489  0.39324886

# Supplying a Poisson GLM log-likelihood explicitly
poisson_loglik <- function(pars) {
  lambda <- exp(model.matrix(glm.D93) %*% pars)
  loglik <- stats::dpois(x = glm.D93$y, lambda = lambda, log = TRUE)
  return(sum(loglik))
}
# This will be a bit slower than profile.glm() because glm.fit() is fast
prof <- profileCI(glm.D93, loglik = poisson_loglik)
prof
#>                   2.5%       97.5%
#> (Intercept)  2.6958271  3.36656379
#> outcome2    -0.8576884 -0.06255514
#> outcome3    -0.6753594  0.08244109
#> treatment2  -0.3932489  0.39324886
#> treatment3  -0.3932489  0.39324886
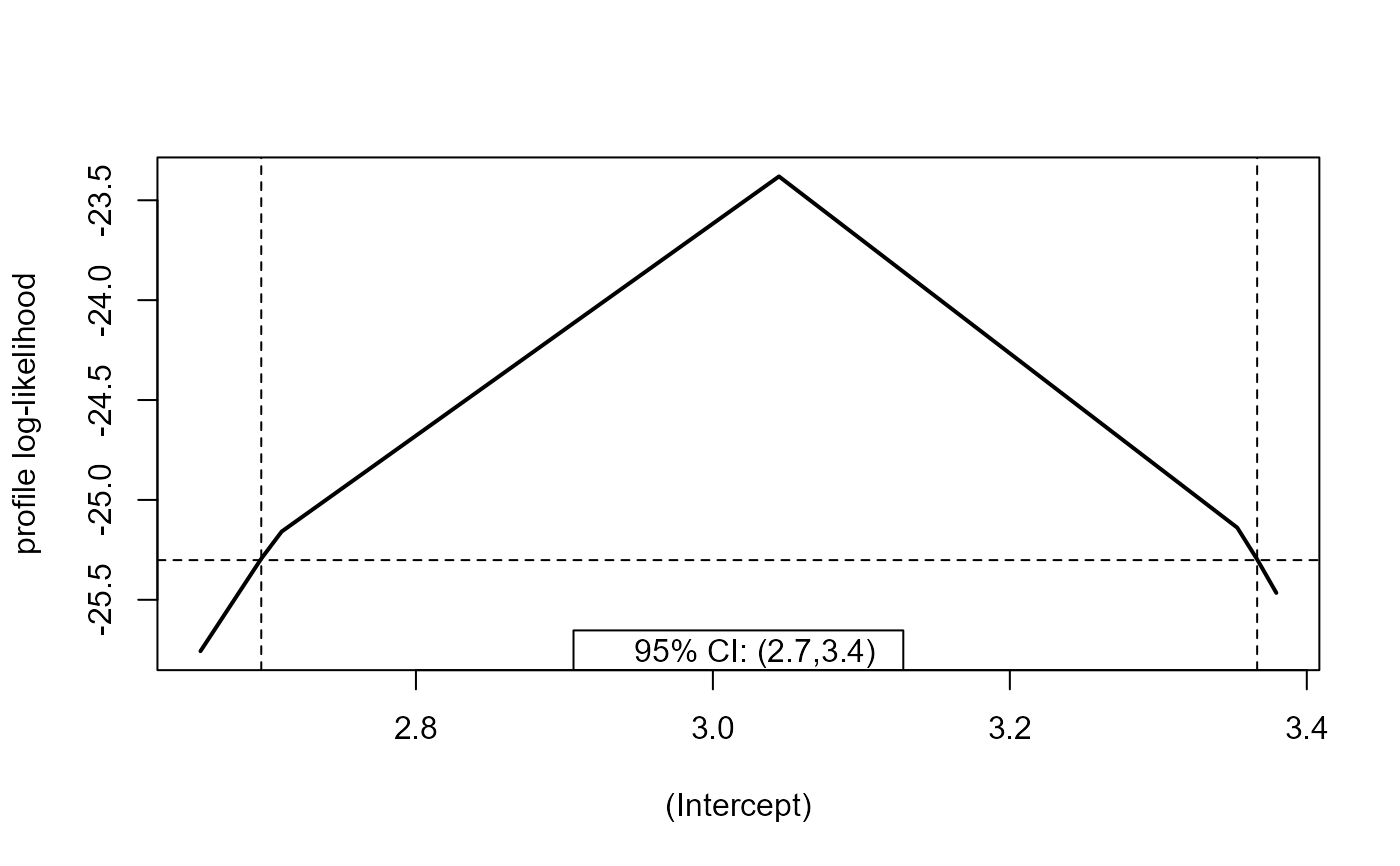
plot(prof, parm = 1)

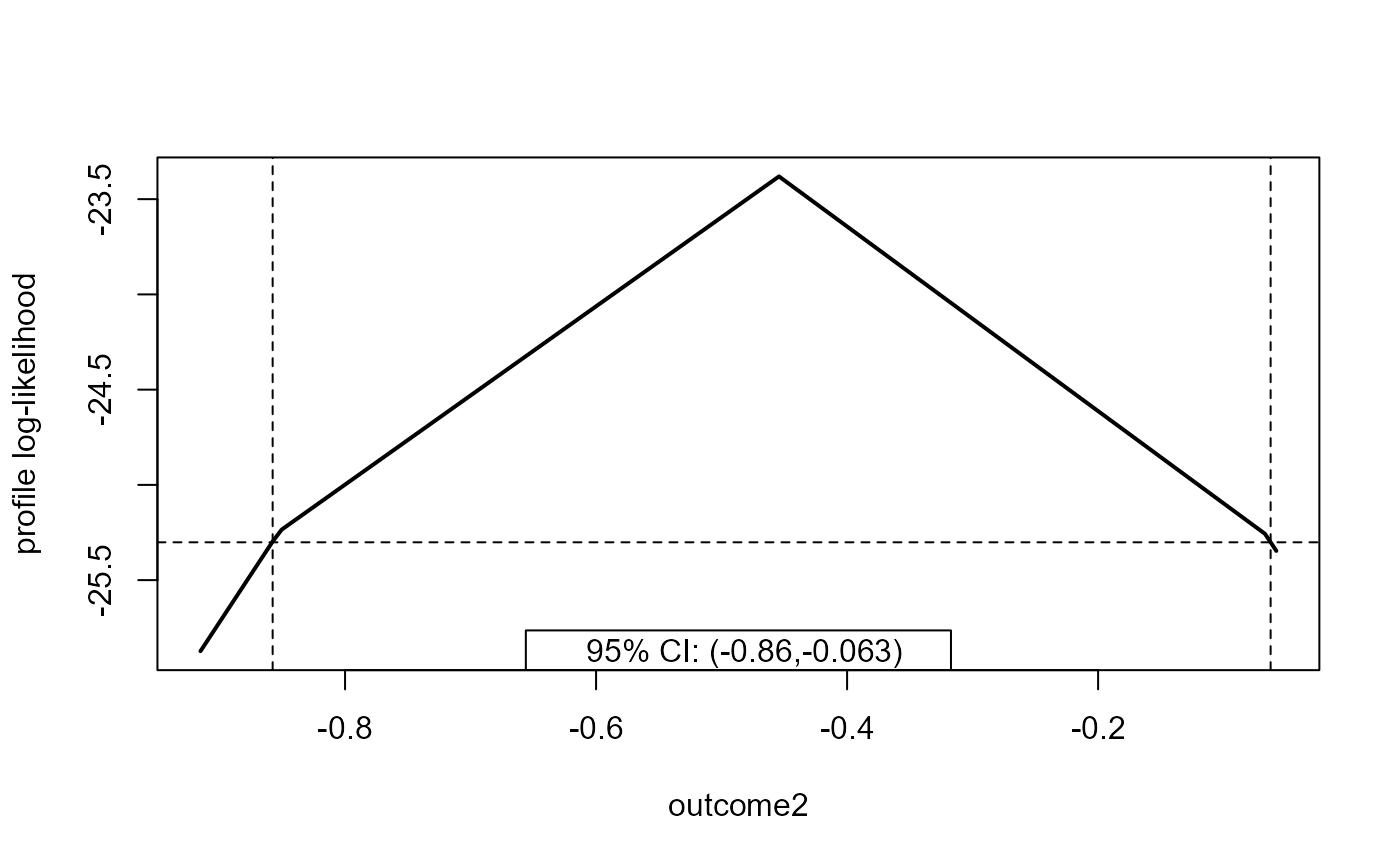
plot(prof, parm = "outcome2")


# Supplying a more general Poisson GLM log-likelihood
poisson_loglik_2 <- function(pars, glm_object) {
  lambda <- exp(model.matrix(glm_object) %*% pars)
  loglik <- stats::dpois(x = glm_object$y, lambda = lambda, log = TRUE)
  return(sum(loglik))
}
prof <- profileCI(glm.D93, loglik = poisson_loglik_2, glm_object = glm.D93)
prof
#>                   2.5%       97.5%
#> (Intercept)  2.6958271  3.36656379
#> outcome2    -0.8576884 -0.06255514
#> outcome3    -0.6753594  0.08244109
#> treatment2  -0.3932489  0.39324886
#> treatment3  -0.3932489  0.39324886

## Nonlinear least squares, from example(nls)
DNase1 <- subset(DNase, Run == 1)
fm1DNase1 <- nls(density ~ SSlogis(log(conc), Asym, xmid, scal), DNase1)
confint(fm1DNase1)
#> Waiting for profiling to be done...
#>           2.5%    97.5%
#> Asym 2.1935437 2.538804
#> xmid 1.3214540 1.678751
#> scal 0.9743072 1.114939
# profileCI() gives slightly different results because confint.nls() is
# not based on profiling the log-likelihood but rather changes in the RSS
prof <- profileCI(fm1DNase1)
#> Error in logLikFn.nls(object, pars = pars, ...): object 'DNase1' not found
prof
#>                   2.5%       97.5%
#> (Intercept)  2.6958271  3.36656379
#> outcome2    -0.8576884 -0.06255514
#> outcome3    -0.6753594  0.08244109
#> treatment2  -0.3932489  0.39324886
#> treatment3  -0.3932489  0.39324886