Skip to contents

Methods for objects of class "evmissing"

Source: R/methods_evmissing.R
evmissing_methods.Rd

Methods for objects of class "evmissing" returned from gev_mle.

Usage

# S3 method for class 'evmissing'
coef(object, ...)

# S3 method for class 'evmissing'
vcov(object, ...)

# S3 method for class 'evmissing'
nobs(object, ...)

# S3 method for class 'evmissing'
logLik(object, ...)

# S3 method for class 'evmissing'
summary(object, digits = max(3, getOption("digits") - 3L), ...)

# S3 method for class 'summary.evmissing'
print(x, ...)

# S3 method for class 'evmissing'
confint(
  object,
  parm = "all",
  level = 0.95,
  profile = FALSE,
  mult = 2,
  faster = FALSE,
  epsilon = 1e-04,
  ...
)

# S3 method for class 'evmissing'
plot(
  x,
  adjust = TRUE,
  which = c("pp", "qq", "return", "density"),
  m = c(2, 10, 100, 1000),
  level = 0.95,
  profile = TRUE,
  num,
  npy = 1,
  ...
)

Arguments

object

An object inheriting from class "evmissing", a result of a call to gev_mle.

...

Further arguments. Only used in the following cases.

  • plot.evmissing: to pass graphical parameters to the graphical functions plot, matplot, abline, lines, matlines and points. In particular, col, lty and lwd may be used to control the colour, type and width of lines and pch the type of plotting symbol. All data points are coloured black in all plots, which cannot be changed.

  • print.summary.evmissing: to pass arguments to print.

digits

An integer. Passed to signif to round the values in the summary.

x

An object returned by summary.evmissing.

parm

A character vector specifying the parameters for which confidence intervals are to be calculated. The default, which = "all", produces confidence intervals for all the parameters, that is, \(\mu\), \(\sigma\) and \(\xi\). Otherwise, parm must be a subset of c("mu", "sigma", "xi").

level

The confidence level required. A numeric scalar in (0, 1).

profile

A logical scalar. If TRUE then confidence intervals based on a profile log-likelihood are returned. If FALSE then intervals based on approximate large sample normal theory, which are symmetric about the MLE, are returned.

mult

A positive numeric scalar. Controls the increment by which the parameter of interest is increased/decreased when profiling above/below its MLE. The increment is mult * se / 100 where se is the estimated standard error of the estimator of the parameter. Decreasing mult profiles at more points but will be slower. The default, mult = 2 should be sufficiently small to produce a smooth looking plot of the profile log-likelihood using plot.confint_gev. To estimate the confidence limits more quickly, the value of mult can be increased and/or the argument faster set to TRUE.

faster

A logical scalar. If faster = TRUE then the profiling of the log-likelihood in search of a lower (upper) confidence limit is started at the corresponding symmetric lower (upper) confidence limit.

epsilon

Only relevant if profile = TRUE. A numeric vector of values that determine the accuracy of the confidence limits. epsilon is recycled to the length of the parameter vector parm.

  • If epsilon[i] > 0 then this value is passed as the argument epsilon to the itp::itp function, which estimates the parameter values for which the profile log-likelihood for parameter i drops to the value that defines the confidence limits, once profiling has been successful in finding an interval within which this value lies.

  • If epsilon[i] < 0 quadratic interpolation is used, which will tend to be faster.

  • If epsilon[i] = 0 then linear interpolation is used, which will be faster still.

adjust

If adjust = TRUE then the diagnostic plots produced by plot.evmissing are adjusted for the number of non-missing observations contributing to each block maximum. Otherwise, no adjustment is made.

which

If supplied, this must either be a character scalar, one of "pp", "qq", "return" or "density" or a numeric scalar in 1:4, with 1 corresponding to "pp" etc. If which is missing then all four plots are produced in a 2 by 2 display.

m

A numeric vector of return periods to label on the horizontal axis of the return level plot. Along with the data, the smallest and largest return period values in m influence the range of return periods for which return level estimates are plotted. All values in m must be greater than 1.

num

An integer scalar. The number of return level estimates to calculate to produce the return level curve and pointwise confidence limits in the return level plot. The default setting is approximately 5 times log(max(m), base = 10). If profile = TRUE then reducing num will speed up the calculation of the confidence limits, at the expense of a reduction in smoothness of the curves.

npy

A numeric scalar. The number \(n_{py}\) of block maxima per year. If the blocks are of length 1 year then npy = 1. This is only used in the return level plot.

Value

coef.evmissing: a numeric vector of length 3 with names c("mu", "sigma", "xi"). The MLEs of the parameters \(\mu\), \(\sigma\) and \(\xi\).

vcov.evmissing: a \(3 \times 3\) matrix with row and column names c("mu", "sigma", "xi"). The estimated variance-covariance matrix for the model parameters \(\mu\), \(\sigma\) and \(\xi\).

nobs.evmissing: a numeric scalar. The number of maxima used in the model fit.

logLik.evmissing: an object of class "logLik": a numeric scalar with value equal to the maximised log-likelihood. The returned object also has attributes nobs, the number of maxima used in the model fit and "df" (degrees of freedom), which is equal to the number of total number of parameters estimated (3).

summary.evmissing: an object with class "summary.evmissing" containing the original function call and a matrix of estimates and estimated standard errors with row names c("mu", "sigma", "xi"). The object is printed by print.summary.evmissing.

print.summary.evmissing: the argument x is returned, invisibly.

confint.evmissing: an object of class c("confint_gev", "evmissing"). A numeric matrix with 2 columns giving the lower and upper confidence limits for each parameter. These columns are labelled as (1-level)/2 and 1-(1-level)/2, expressed as a percentage, by default 2.5% and 97.5%. The row names are the names of the parameters supplied in parm. The ordering "mu", "sigma", "xi" is retained regardless of the ordering of the parameters in parm. If profile = TRUE then the returned object has extra attributes crit, level and for_plot. The latter is a named list of length 3 with components mu, sigma and xi. Each components is a 2-column numeric matrix. The first column (named mu_values etc) contains values of the parameter and the second column the corresponding values of the profile log-likelihood. The profile log-likelihood is equal to the attribute crit at the limits of the confidence interval. The attribute level is the input argument level.

plot.evmissing: if a return level plot has been requested, a 3-column matrix containing the values plotted in the return level plot. Column 2 contains the estimated return levels and columns 1 and 3 the lower and upper confidence limits.

Details

The plots produced by plot.evmissing are of a similar form to the visual diagnostics is the ismev package and described in Coles (2001), that is, a probability plot (which = "pp" or which = 1), a quantile plot (which ="qq" of which = 2), a return level plot (which = "return" or which = 3) and a histogram of block maxima with a fitted GEV density superimposed (which = "density" or which = 4). Pointwise confidence bands of level level are added to the probability plot and quantile plot.

The default setting for confidence intervals for a return level plot produced by plot.evmissing is profile = TRUE, which uses gev_return and confint.return_level. The plot takes longer to produce, but it avoids the unrealistic feature of the lower confidence limits decreasing as we extrapolate to long return periods.

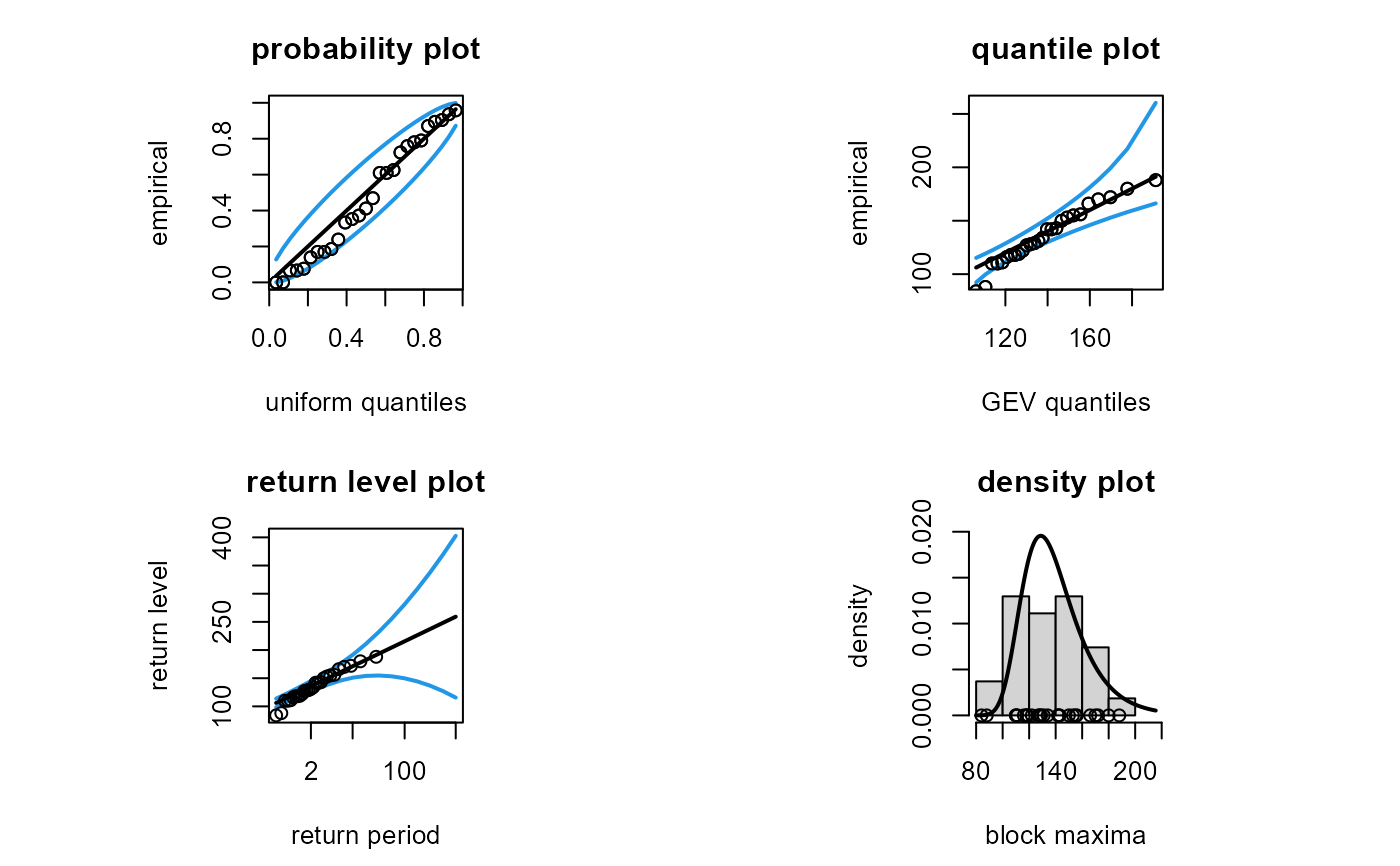
If adjust = TRUE then the empirical values based on the observed block maxima are adjusted for the number of non-missing raw observations in each block based on the fitted GEV parameter values for reduced block sizes. Passing adjust = FALSE is not sensible, but, if there are missing data, then it can serve to show that making the adjustment is necessary to give the correct impression of how well the model has fitted the data.

For confint.evmissing, the default, epsilon = -1, should work well enough in most circumstances, but to achieve a specific accuracy set epsilon to be a small positive value, for example, epsilon = 1e-4.

References

Coles, S. G. (2001) An Introduction to Statistical Modeling of Extreme Values, Springer-Verlag, London. doi:10.1007/978-1-4471-3675-0_3

Heffernan, J. E. and Stephenson, A. G. (2018). ismev: An Introduction to Statistical Modeling of Extreme Values. R package version 1.42. doi:10.32614/CRAN.package.ismev

See also

gev_mle and confint_gev_methods.

Examples

## Plymouth ozone data

# Make adjustment for the numbers of non-missing values per block
fit <- gev_mle(PlymouthOzoneMaxima)
coef(fit)
#>           mu        sigma           xi 
#> 1.287713e+02 1.880807e+01 1.099327e-03 
vcov(fit)
#>               mu      sigma          xi
#> mu    19.3747981 4.20796047 -0.29507393
#> sigma  4.2079605 6.94147798  0.01825292
#> xi    -0.2950739 0.01825292  0.02512590
nobs(fit)
#> [1] 27
logLik(fit)
#> 'log Lik.' -120.5328 (df=3)
summary(fit)
#> 
#> Call:
#> gev_mle(data = PlymouthOzoneMaxima)
#> 
#>        Estimate Std. Error
#> mu    1.288e+02     4.4020
#> sigma 1.881e+01     2.6350
#> xi    1.099e-03     0.1585

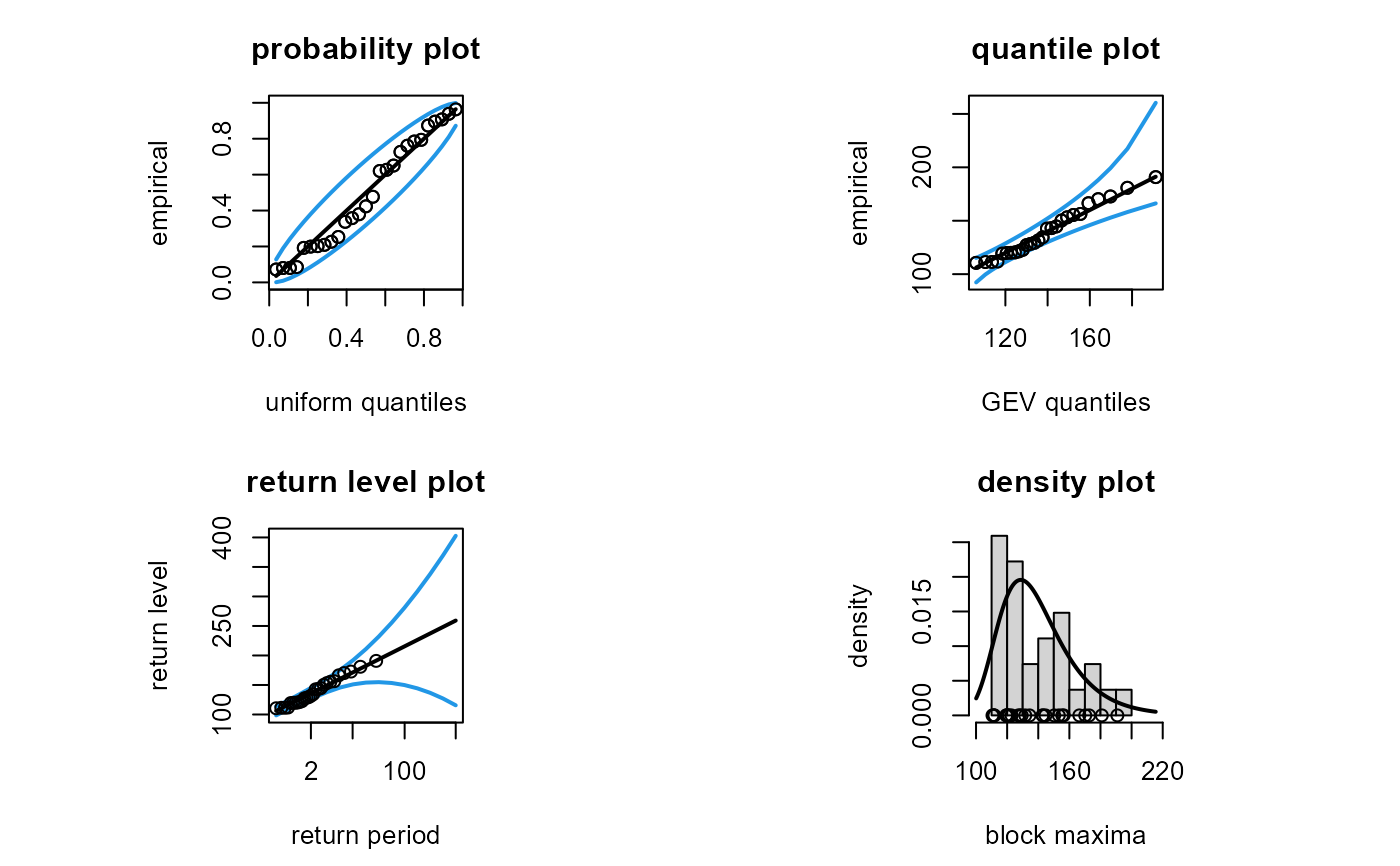
## Model diagnostic plots

# When profile = FALSE the return confidence limits are unrealistic
# for long return periods
plot(fit, profile = FALSE)


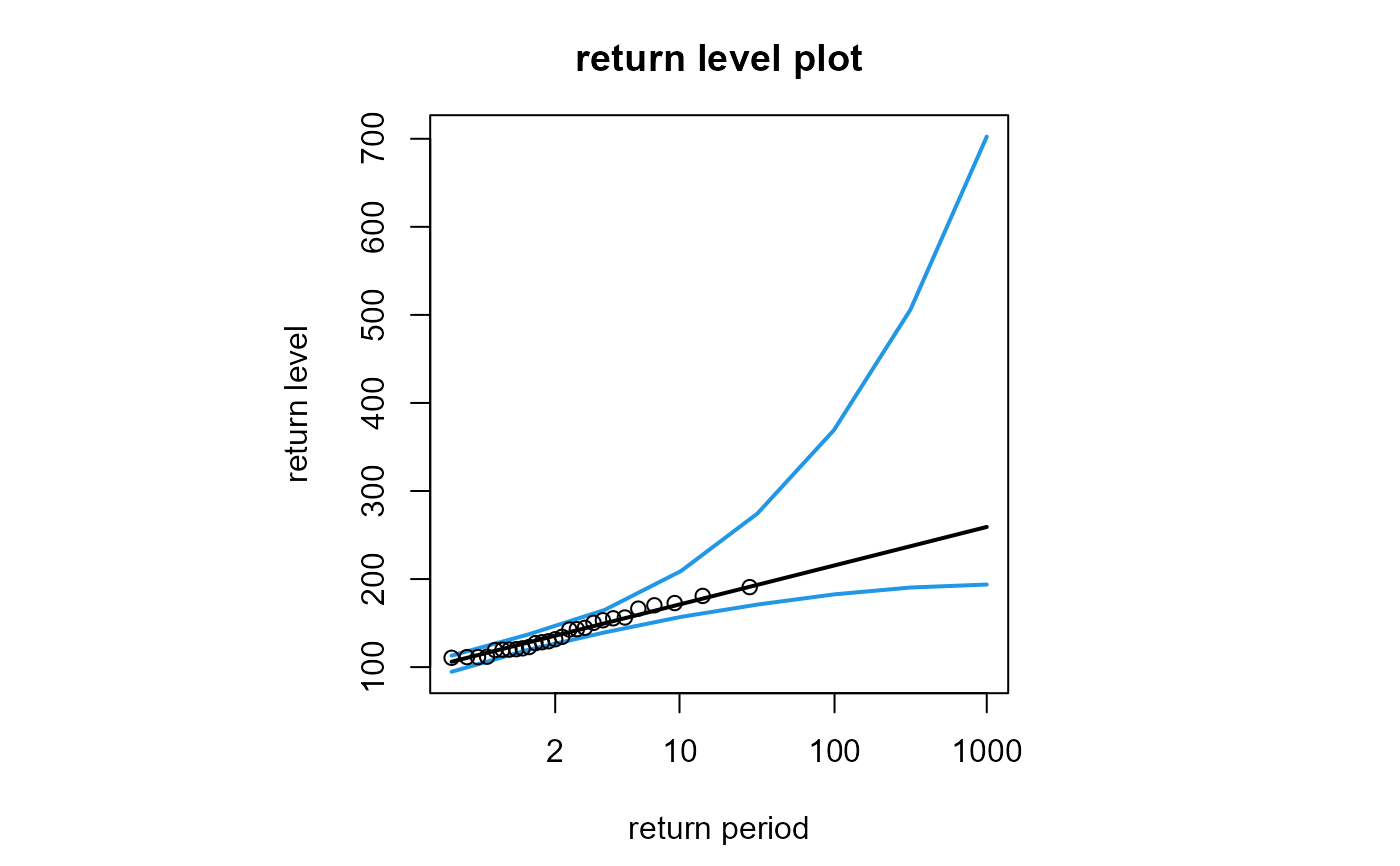
# Create the return level plot only
# When profile = TRUE (the default) the confidence limits are fine
# but the plot takes longer
# For speed, we reduce the number, num, of points used to plot the curves
plot(fit, which = 3, num = 8)


# If we do not reflect the adjustment in the plot then it gives a false
# impression of how well the model has fitted the data
plot(fit, adjust = FALSE, profile = FALSE)


## Confidence intervals

# Confidence limits that are symmetric about the respective MLEs
confint(fit)
#>              2.5%       97.5%
#> mu    120.1441804 137.3984539
#> sigma  13.6442183  23.9719290
#> xi     -0.3095775   0.3117762

# Calling confint to produce a smooth profile log-likelihood plot
x <- confint(fit, profile = TRUE)
x
#>              2.5%       97.5%
#> mu    120.3550195 137.9594426
#> sigma  14.5976855  25.5383429
#> xi     -0.3237415   0.3159855
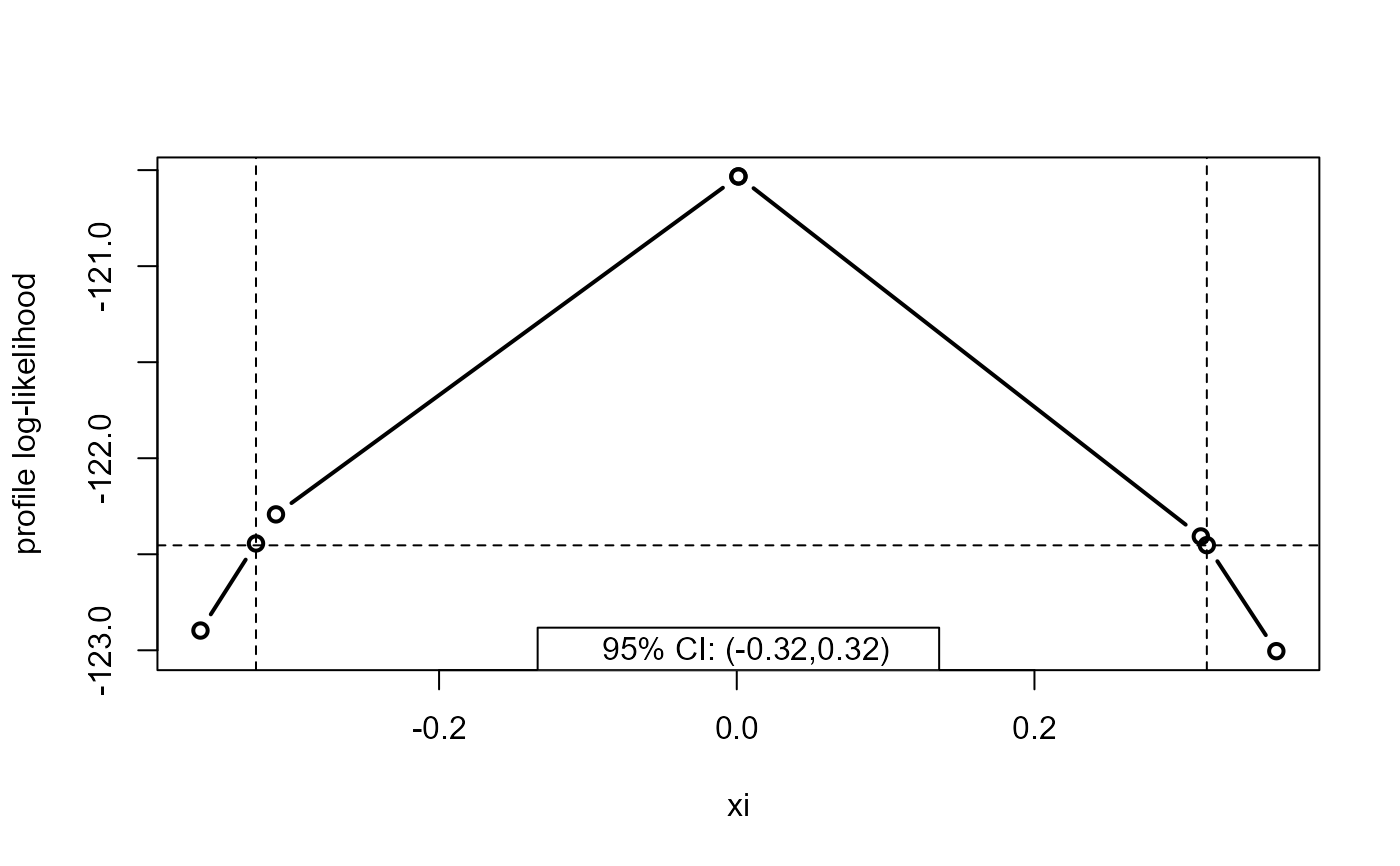
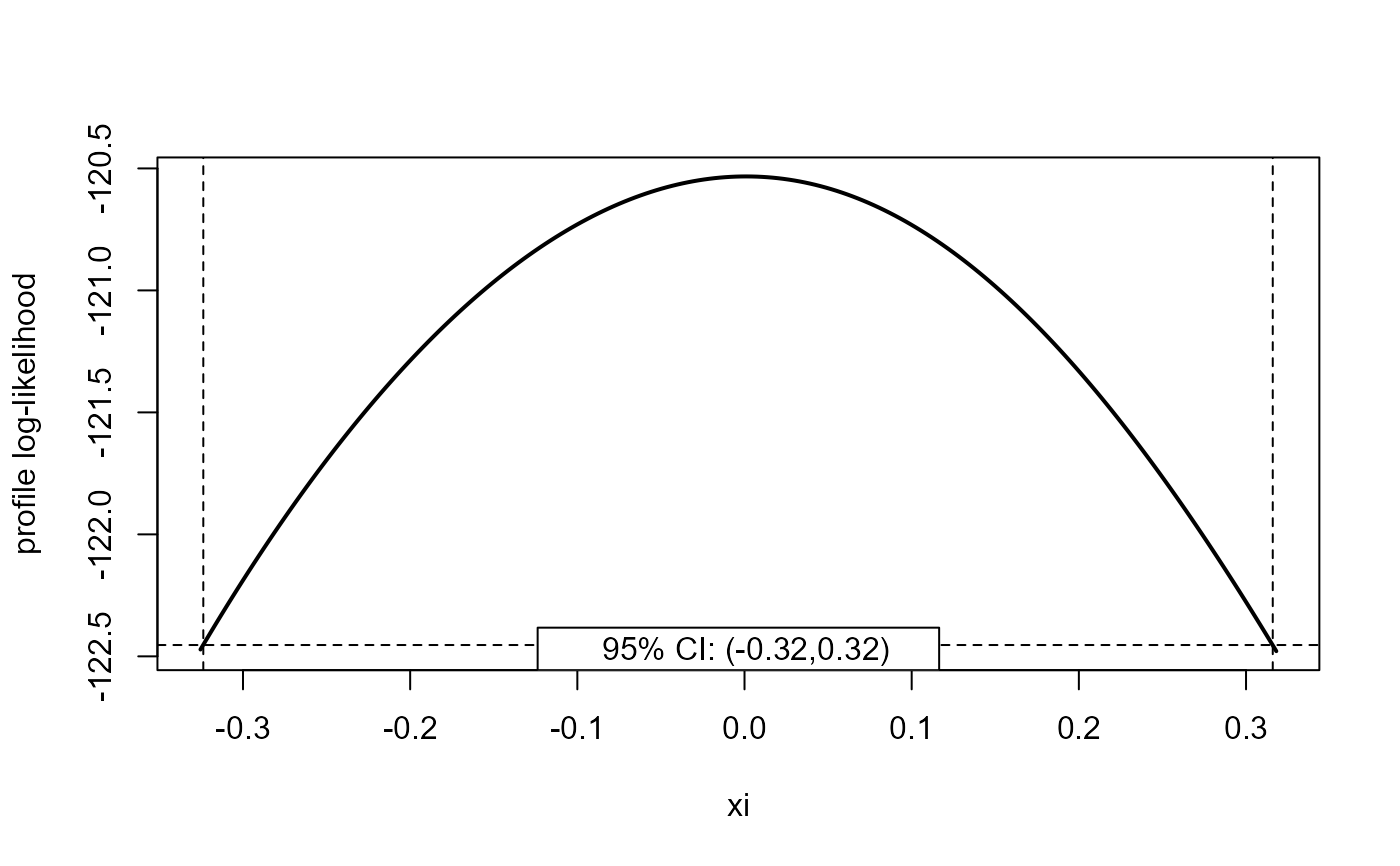
plot(x, parm = "xi")


# Doing this more quickly when we only want the approximate confidence limits
x <- confint(fit, profile = TRUE, mult = 32, faster = TRUE)
x
#>              2.5%       97.5%
#> mu    120.3574766 137.9594215
#> sigma  14.8182568  25.5383840
#> xi     -0.3229961   0.3158122
plot(x, parm = "xi", type = "b")