Loglikelihood adjustment using the sandwich estimator

Performs adjustments of a user-supplied independence loglikelihood for the presence of cluster dependence, following Chandler and Bate (2007). The user provides a function that returns a vector of observation-specific loglikelihood contributions and a vector that indicates cluster membership. The loglikelihood of a sub-model can be adjusted by fixing a set of parameters at particular values.

Usage

adjust_loglik(
  loglik = NULL,
  ...,
  cluster = NULL,
  p = NULL,
  init = NULL,
  par_names = NULL,
  fixed_pars = NULL,
  fixed_at = 0,
  name = NULL,
  larger = NULL,
  alg_deriv = NULL,
  alg_hess = NULL,
  mle = NULL,
  H = NULL,
  V = NULL
)

Arguments

loglik

A named function. Returns a vector of the loglikelihood contributions of individual observations. The first argument must be the vector of model parameter(s). If any of the model parameters are out-of-bounds then loglik should return either -Inf or a vector with at least one element equal to -Inf. The number of parameters in the full model must be specified using (at least) one of the arguments p, init or par_names.

...

Further arguments to be passed either to loglik (and to alg_deriv and alg_hess if these are supplied) or to optim. The latter may include gr, method, lower, upper or control. In the call to optim, hessian = TRUE will be used regardless of any value supplied. The function loglik must not have arguments with names that match any of these arguments to optim.

cluster

A vector or factor indicating from which cluster the respective loglikelihood contributions from loglik originate. Must have the same length as the vector returned by loglik. If cluster is not supplied then it is set inside adjust_loglik under the assumption that each observation forms its own cluster.

p

A numeric scalar. The dimension of the full parameter vector, i.e. the number of parameters in the full model. Must be consistent with the lengths of init and par_names, if these are also supplied.

init

A numeric vector of initial values. Must have length equal to the number of parameters in the full model. If init is supplied then p is set to length(init), provided that this is consistent with the the value given by p or implied by length(par_names). If fixed_pars is not NULL then init[-fixed_pars] is used in the search for the MLE. If init is not supplied then rep(0.1, p) is used.

par_names

A character vector. Names of the p parameters in the full model. Must be consistent with the lengths of init and p, if these are also supplied.

fixed_pars

A vector specifying which parameters are to be restricted to be equal to the value(s) in fixed_at. Can be either a numeric vector, specifying indices of the components of the full parameter vector, or a character vector of parameter names, which must be a subset of those supplied in par_names or stored in the object larger.

fixed_at

A numeric vector of length 1 or length(fixed_pars). If length(fixed_at) = 1 then the components fixed_pars of the parameter vector are all fixed at fixed_at. If length(fixed_at) = length(fixed_pars) then the component fixed_pars[i] is fixed at fixed_at[i] for each i.

name

A character scalar. A name for the model that gives rise to loglik. If this is not supplied then the name in larger is used, if this has been supplied, and the name of the function loglik otherwise.

larger

Only relevant if fixed_pars is not NULL. If larger is supplied but fixed_pars is not then an error will result. if larger is supplied then information about the model in larger, e.g. about p and par_names will override any attempt to set these arguments in the call to adjust_loglik.

An object of class "chandwich" returned by adjust_loglik, corresponding to a model in which the smaller model implied by fixed_pars is nested. If larger is supplied then all the arguments to adjust_loglik apart from fixed_pars and fixed_at are extracted from larger. If init is not supplied in the current call to adjust_loglik then init is set to attr(larger, "MLE"), with the elements in fixed_pars set to fixed_at.

alg_deriv

A function with the vector of model parameter(s) as its first argument. Returns a length(cluster) by p numeric matrix. Column i contains the derivatives of each of the loglikelihood contributions in loglik with respect to model parameter i.

alg_hess

A function with the vector of model parameter(s) as its first argument. Returns a p by p numeric matrix equal to the Hessian of loglik, i.e. the matrix of second derivatives of the function loglik.

Supplying both V and alg_deriv or both H and alg_hess will produce an error.

mle

A numeric vector. Can only be used if fixed_pars = NULL. Provides the maximum likelihood estimate of the model parameters, that is, the value of the parameter vector at which the independence loglikelihood loglik is maximized. Must have length equal to the number of parameters in the full model. If mle is supplied then p is set to length(mle), provided that this is consistent with the the value given by p or implied by length(par_names). If mle is supplied then it overrides init.

H, V

p by p numeric matrices. Only used if mle is supplied. Provide estimates of the Hessian of the independence loglikelihood (H) and the variance of the vector of cluster-specific contributions to the score vector (first derivatives with respect to the parameters) of the independence loglikelihood, each evaluated at the MLE mle. See the Introducing chandwich vignette and/or Chandler and Bate (2007).

Supplying both V and alg_deriv or both H and alg_hess will produce an error.

Value

A function of class "chandwich" to evaluate an adjusted loglikelihood, or the independence loglikelihood, at one or more sets of model parameters, with arguments

x: A numeric vector or matrix giving values of the p_current (see below) parameters in the model to which the returned adjusted loglikelihood applies. If p_current = 1 this may be a numeric vector or a matrix with 1 column. If p_current > 1 this may be a numeric vector of length p (one set of model parameters) or a numeric matrix with p columns (nrow(x) sets of model parameters), one set in each row of x.
type: A character scalar. The type of adjustment to use. One of "vertical", "cholesky", "spectral" or "none".

The latter results in the evaluation of the (unadjusted) independence loglikelihood. The function has (additional) attributes

p_full, p_current: The number of parameters in the full model and current models, respectively.
free_pars: A numeric vector giving the indices of the free parameters in the current model, with names inferred from par_names if this was supplied.
MLE, res_MLE: Numeric vectors, with names inferred from par_names if this was supplied. Maximum likelihood estimates of free parameters under the current model (mle) and all parameters in the full model, including any parameters with fixed values (res_MLE).
SE, adjSE: The unadjusted and adjusted estimated standard errors, of the free parameters, respectively.
VC, adjVC: The unadjusted and adjusted estimated variance-covariance matrix of the free parameters, respectively.
HI, HA: The Hessians of the independence and adjusted loglikelihood, respectively.
C_cholesky, C_spectral: The matrix C in equation (14) of Chandler and Bate (2007), calculated using Cholesky decomposition and spectral decomposition, respectively.
full_par_names, par_names: The names of the parameters in the full and current models, respectively, if these were supplied in this call or a previous call.
max_loglik: The common maximised value of the independence and adjusted loglikelihoods.
loglik, cluster: The arguments loglik and cluster supplied in this call, or a previous call.
loglik_args: A list containing the further arguments passed to loglik via ... in this call, or a previous call.
loglikVecMLE: a vector containing the contributions of individual observations to the independence log-likelihood evaluated at the MLE.
name: The argument name, or the name of the function loglik if name isn't supplied.
nobs: The number of observations.
call: The call to adjust_loglik.

If fixed_pars is not NULL then there are further attributes

fixed_pars: The argument fixed_pars, with names inferred from par_names if this was supplied.
fixed_at: The argument fixed_at, with names inferred from par_names if this was supplied.

If alg_deriv and/or alg_hess were supplied then these are returned as further attributes.

To view an individual attribute called att_name use attr(x, "att_name") or attributes(x)$att_name.

Details

Three adjustments to the independence loglikelihood described in Chandler and Bate (2007) are available. The vertical adjustment is described in Section 6 and two horizontal adjustments are described in Sections 3.2 to 3.4. See the descriptions of type and, for the horizontal adjustments, the descriptions of C_cholesky and C_spectral, in Value.

The adjustments involve first and second derivatives of the loglikelihood with respect to the model parameters. These are estimated using jacobian and optimHess unless alg_deriv and/or alg_hess are supplied.

References

Chandler, R. E. and Bate, S. (2007). Inference for clustered data using the independence loglikelihood. Biometrika, 94(1), 167-183. doi:10.1093/biomet/asm015

Examples

# ------------------------- Binomial model, rats data ----------------------

# Contributions to the independence loglikelihood
binom_loglik <- function(prob, data) {
  if (prob < 0 || prob > 1) {
    return(-Inf)
  }
  return(dbinom(data[, "y"], data[, "n"], prob, log = TRUE))
}
rat_res <- adjust_loglik(loglik = binom_loglik, data = rats, par_names = "p")

# Plot the loglikelihoods
plot(rat_res, type = 1:4, legend_pos = "bottom", lwd = 2, col = 1:4)

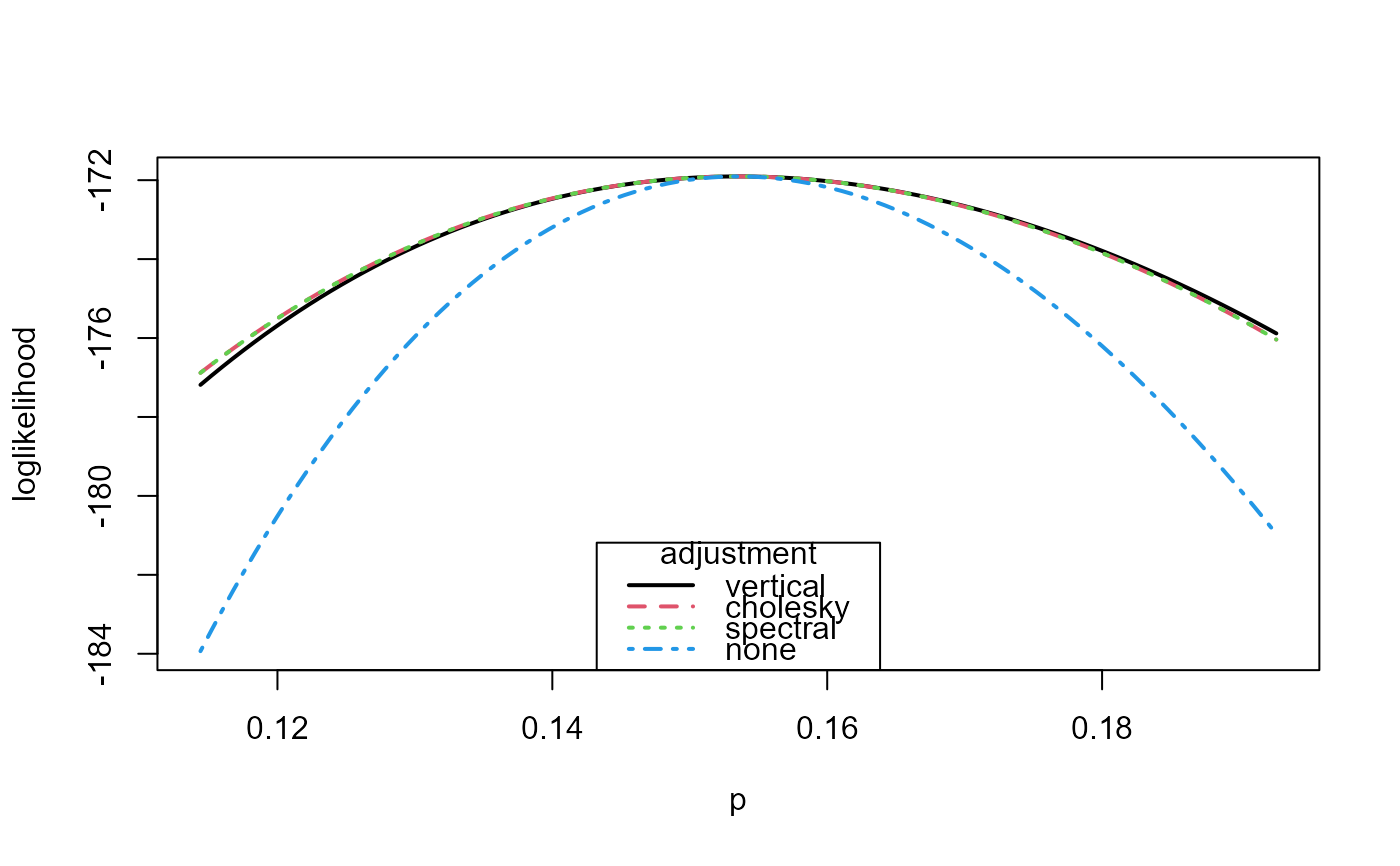# MLE, SEs and adjusted SEs
summary(rat_res)
#>      MLE       SE adj. SE
#> p 0.1535 0.008645 0.01305

# -------------------------- GEV model, owtemps data -----------------------
# ------------ following Section 5.2 of Chandler and Bate (2007) -----------

# Contributions to the independence loglikelihood
gev_loglik <- function(pars, data) {
  o_pars <- pars[c(1, 3, 5)] + pars[c(2, 4, 6)]
  w_pars <- pars[c(1, 3, 5)] - pars[c(2, 4, 6)]
  if (isTRUE(o_pars[2] <= 0 | w_pars[2] <= 0)) return(-Inf)
  o_data <- data[, "Oxford"]
  w_data <- data[, "Worthing"]
  check <- 1 + o_pars[3] * (o_data - o_pars[1]) / o_pars[2]
  if (isTRUE(any(check <= 0))) return(-Inf)
  check <- 1 + w_pars[3] * (w_data - w_pars[1]) / w_pars[2]
  if (isTRUE(any(check <= 0))) return(-Inf)
  o_loglik <- log_gev(o_data, o_pars[1], o_pars[2], o_pars[3])
  w_loglik <- log_gev(w_data, w_pars[1], w_pars[2], w_pars[3])
  return(o_loglik + w_loglik)
}

# Initial estimates (method of moments for the Gumbel case)
sigma <- as.numeric(sqrt(6 * diag(var(owtemps))) / pi)
mu <- as.numeric(colMeans(owtemps) - 0.57722 * sigma)
init <- c(mean(mu), -diff(mu) / 2, mean(sigma), -diff(sigma) / 2, 0, 0)

# Loglikelihood adjustment for the full model
par_names <- c("mu[0]", "mu[1]", "sigma[0]", "sigma[1]", "xi[0]", "xi[1]")
large <- adjust_loglik(gev_loglik, data = owtemps, init = init,
                       par_names = par_names)
# Rows 1, 3 and 4 of Table 2 of Chandler and Bate (2007)
t(summary(large))
#>           mu[0]  mu[1] sigma[0] sigma[1]    xi[0]    xi[1]
#> MLE     81.1700 2.6680   3.7290   0.5312 -0.19890 -0.08835
#> SE       0.3282 0.3282   0.2293   0.2293  0.04937  0.04937
#> adj. SE  0.4036 0.2128   0.2426   0.1911  0.03943  0.03625

# Loglikelihood adjustment of some smaller models: xi[1] = 0 etc

# Starting from a larger model
medium <- adjust_loglik(larger = large, fixed_pars = "xi[1]")
small <- adjust_loglik(larger = large, fixed_pars = c("sigma[1]", "xi[1]"))
small <- adjust_loglik(larger = medium, fixed_pars = c("sigma[1]", "xi[1]"))

# Starting from scratch
medium <- adjust_loglik(gev_loglik, data = owtemps, init = init,
          par_names = par_names, fixed_pars = "xi[1]")
small <- adjust_loglik(gev_loglik, data = owtemps, init = init,
         par_names = par_names, fixed_pars = c("sigma[1]", "xi[1]"))

# --------- Misspecified Poisson model for negative binomial data ----------

# ... following Section 5.1 of the "Object-Oriented Computation of Sandwich
# Estimators" vignette of the sandwich package
# https://cran.r-project.org/web/packages/sandwich/vignettes/sandwich-OOP.pdf

# Simulate data
set.seed(123)
x <- rnorm(250)
y <- rnbinom(250, mu = exp(1 + x), size = 1)
# Fit misspecified Poisson model
fm_pois <- glm(y ~ x + I(x^2), family = poisson)
summary(fm_pois)$coefficients
#>                Estimate Std. Error   z value      Pr(>|z|)
#> (Intercept)  1.06326821 0.04135723 25.709367 9.184267e-146
#> x            0.99607219 0.05353446 18.606186  2.862861e-77
#> I(x^2)      -0.04912373 0.02314608 -2.122335  3.380961e-02

# Contributions to the independence loglikelihood
pois_glm_loglik <- function(pars, y, x) {
  log_mu <- pars[1] + pars[2] * x + pars[3] * x ^ 2
  return(dpois(y, lambda = exp(log_mu), log = TRUE))
}
pars <- c("alpha", "beta", "gamma")
pois_quad <- adjust_loglik(pois_glm_loglik, y = y, x = x, par_names = pars)
summary(pois_quad)
#>            MLE      SE adj. SE
#> alpha  1.06300 0.04136 0.08378
#> beta   0.99610 0.05354 0.10520
#> gamma -0.04913 0.02315 0.03628

# Providing algebraic derivatives and Hessian
pois_alg_deriv <- function(pars, y, x) {
  mu <- exp(pars[1] + pars[2] * x + pars[3] * x ^ 2)
  return(cbind(y - mu, x * (y - mu), x ^2 * (y - mu)))
}
pois_alg_hess <- function(pars, y, x) {
  mu <- exp(pars[1] + pars[2] * x + pars[3] * x ^ 2)
  alg_hess <- matrix(0, 3, 3)
  alg_hess[1, ] <- -c(sum(mu), sum(x * mu), sum(x ^ 2 * mu))
  alg_hess[2, ] <- -c(sum(x * mu), sum(x ^ 2 * mu), sum(x ^ 3 * mu))
  alg_hess[3, ] <- -c(sum(x ^ 2 * mu), sum(x ^ 3 * mu), sum(x ^ 4 * mu))
  return(alg_hess)
}
pois_quad <- adjust_loglik(pois_glm_loglik, y = y, x = x, p = 3,
                           alg_deriv = pois_alg_deriv, alg_hess = pois_alg_hess)
summary(pois_quad)
#>        MLE      SE adj. SE
#> 1  1.06300 0.04136 0.08378
#> 2  0.99610 0.05354 0.10520
#> 3 -0.04913 0.02315 0.03628

got_sandwich <- requireNamespace("sandwich", quietly = TRUE)
if (got_sandwich) {
  # Providing MLE, H and V
  # H and V calculated using bread() and meat() from sandwich package
  n_obs <- stats::nobs(fm_pois)
  pois_quad <- adjust_loglik(pois_glm_loglik, y = y, x = x, p = 3,
                             mle = fm_pois$coefficients,
                             H = -solve(sandwich::bread(fm_pois) / n_obs),
                             V = sandwich::meat(fm_pois) * n_obs)
}