An overview of donut

Paul Northrop

2023-09-02

Source: vignettes/donut-vignette.Rmd

Nearest Neighbour Search with Variables on a Torus

A non-parametric method for classification or regression involves making inferences locally using the \(k\) observations closest to a point of interest, based on some metric, such as L2 or L1. There are several R packages, such as RANN (Arya et al. 2019) and nabor (Elseberg et al. 2012), that find \(k\) nearest neighbours. The donut package considers the situation where one or more of the variables in the dataset is periodic on a finite interval. For example, direction is periodic on the interval \((0, 360)\) degrees. In the small dataset \(\{10, 90, 350\}\) degrees 350 is closer to 10 than is 90: 10 and 350 are separated by 20 degrees, 10 and 90 by 80 degrees.

The function nnt() finds the \(k\) nearest neighbours of each of a set of points of interest, wrapping periodic variables on a torus so that this periodicity is reflected. The user chooses the function to use to find the nearest neighbours. The nearest neighbour functions from the aforementioned packages are used as examples.

An example

We use a simple 2-dimensional example from the RANN::nn2() documentation. For the purposes of illustrating nnt() we will suppose that one of more of the variables in periodic. In one or two dimensions the plot method associated with nnt() can be used to show the effect of taking this periodicity into account.

library(donut)
set.seed(20092019)
x1 <- runif(100, 0, 2 * pi)
x2 <- runif(100, 0, 3)
DATA <- data.frame(x1, x2)

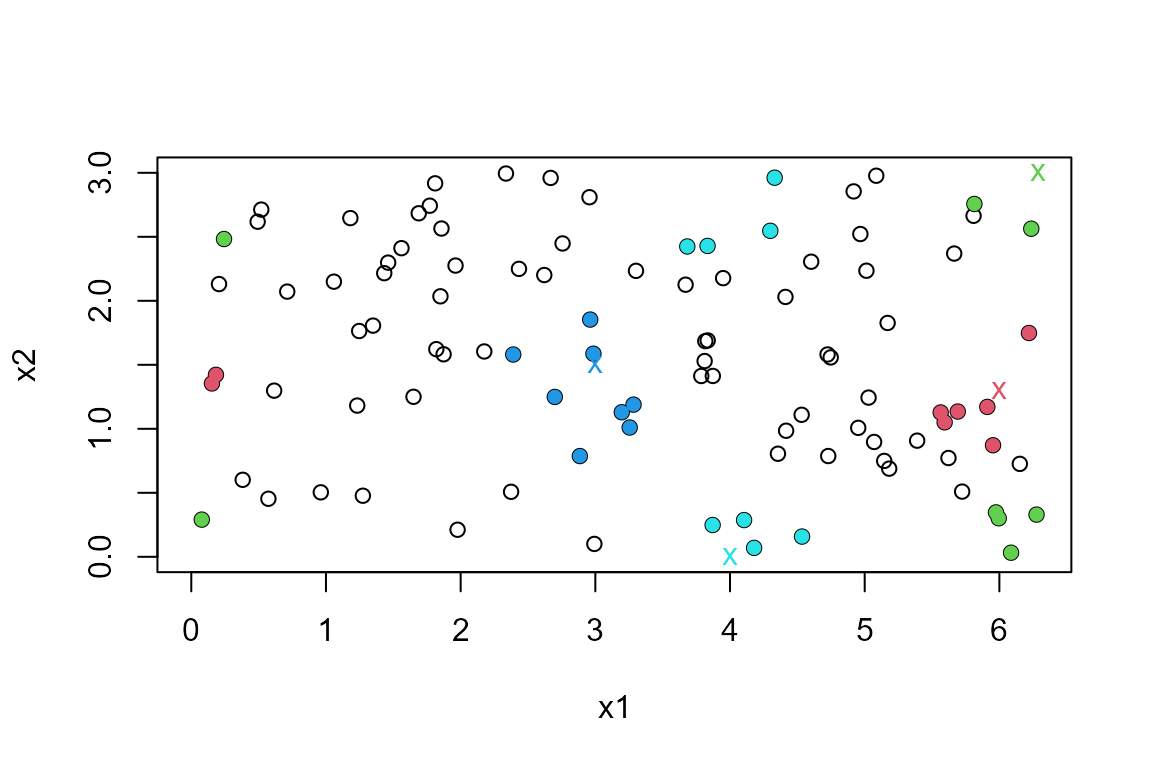
First, we suppose that only x1 should be wrapped, on the range \((0, 2\pi)\). We use a small number of query points of interest, chosen to illustrate the wrapping. By default RANN::nn2(), which uses the L2 metric, is used to find the nearest neighbours. In the plot, query points are indicated with colour-coded crosses and the 8 nearest neighbours of each point are shaded in the same colour. The wrapping of the variable x1 is apparent.

library(RANN)
#> Warning: package 'RANN' was built under R version 4.2.3
ranges1 <- c(0, 2 * pi)
query1 <- rbind(c(6, 1.3), c(2 * pi, 3), c(3, 1.5), c(4, 0))
res1 <- nnt(DATA, query1, k = 8, torus = 1, ranges = ranges1)
plot(res1, ylim = c(0, 3))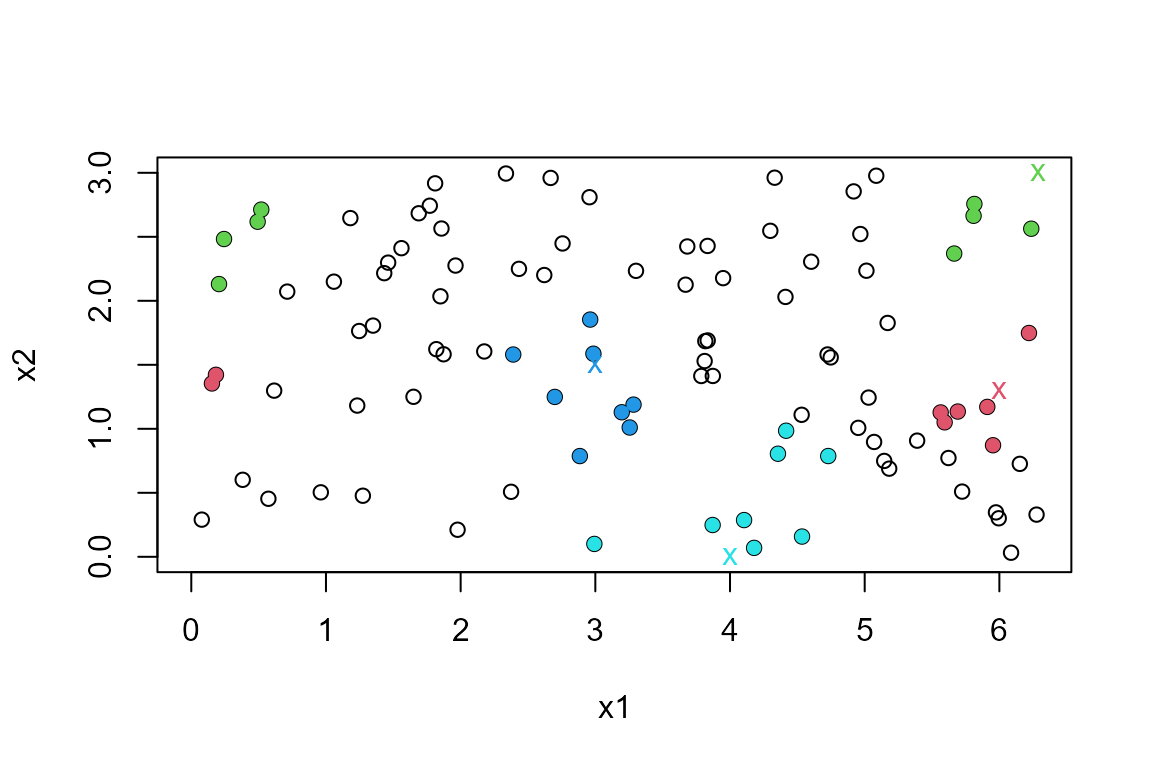

The object returned from nnt() is a list including the same components that are returned from RANN::nn2() and nabor::knn(), that is, matrices containing the nearest neighbour distances (nn.dists) and the corresponding indices in data (nn.idx). The \(i\)th row relates to the \(i\)th query point, the \(i\)th row of query.

res1$nn.dists
#>            [,1]      [,2]      [,3]      [,4]      [,5]      [,6]      [,7]
#> [1,] 0.15704522 0.3501943 0.4310847 0.4397544 0.4685137 0.4767617 0.4819253
#> [2,] 0.43932258 0.5283214 0.5716203 0.5815153 0.5939273 0.6234609 0.8834840
#> [3,] 0.08775281 0.3553781 0.3918241 0.4196264 0.4209570 0.5525234 0.6148038
#> [4,] 0.19200301 0.2799162 0.3053224 0.5576230 0.8803338 1.0122411 1.0694339
#>           [,8]
#> [1,] 0.4993756
#> [2,] 0.8933141
#> [3,] 0.7221735
#> [4,] 1.0731836
res1$nn.idx
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
#> [1,]   54   18    8   27   19   30   31   28
#> [2,]   63   82   74   58   81   45   42   88
#> [3,]   25   37    6   41   89    7   80   33
#> [4,]   93   87   52   12   29   85    1   40

Now we suppose that both variables should be wrapped, on the ranges \((0, 2\pi)\) and \((0, 3)\) respectively. The points shaded in green illustrate the effect of wrapping in both variables.

ranges <- rbind(c(0, 2 * pi), c(0, 3))
query <- rbind(c(6, 1.3), c(2 * pi, 3), c(3, 1.5), c(4, 0))
res2 <- nnt(DATA, query, k = 8, torus = 1:2, ranges = ranges)
plot(res2)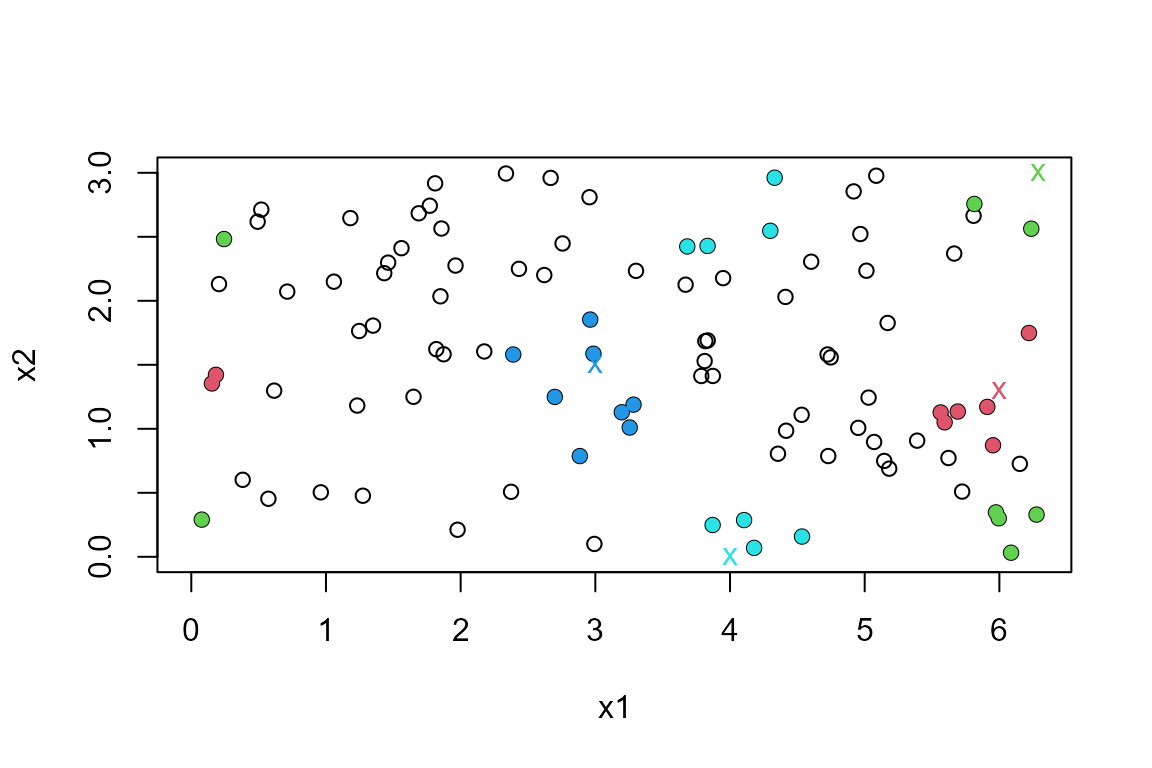

The argument fn can be used to choose the function that finds nearest neighbour distances. For example, we could choose nabor::knn(). Any function can be used provided that it has syntax consistent with a call fn(data = data, query = query, k = k, ...). The following code produce the same output as fn = RANN::nn2.

library(nabor)
#> Warning: package 'nabor' was built under R version 4.2.3
ranges <- rbind(c(0, 2 * pi), c(0, 3))
query <- rbind(c(6, 1.3), c(2 * pi, 3), c(3, 1.5), c(4, 0))
res2 <- nnt(DATA, query, k = 8, fn = nabor::knn, torus = 1:2, ranges = ranges)
plot(res2)

References

Arya, Sunil, David Mount, Samuel E. Kemp, and Gregory Jefferis. 2019. RANN: Fast Nearest Neighbour Search (Wraps ANN Library) Using L2 Metric. https://CRAN.R-project.org/package=RANN.
Elseberg, J., S. Magnenat, R. Siegwart, and A. Nüchter. 2012. “Comparison of Nearest-Neighbor-Search Strategies and Implementations for Efficient Shape Registration.” Journal of Software Engineering for Robotics (JOSER) 3 (1): 2–12. https://CRAN.R-project.org/package=nabor.