Confidence intervals for the extremal index $\theta$ for "spm" objects

confint method for objects of class c("spm", "exdex"). Computes confidence intervals for $\theta$ based on an object returned from spm. Two types of interval may be returned: (a) intervals that are based on approximate large-sample normality of the estimators of $\theta$ (or of $\log\theta$ if conf_scale = "log"), and which are symmetric about the respective point estimates, and (b) likelihood-based intervals based on an adjustment of a naive (pseudo-) loglikelihood, using the adjust_loglik function in the chandwich package. The plot method plots the log-likelihood for $\theta$, with the required confidence interval(s) indicated on the plot.

Usage

# S3 method for class 'spm'
confint(
  object,
  parm = "theta",
  level = 0.95,
  maxima = c("sliding", "disjoint"),
  interval_type = c("norm", "lik", "both"),
  conf_scale = c("theta", "log"),
  constrain = TRUE,
  bias_adjust = TRUE,
  type = c("vertical", "cholesky", "spectral", "none"),
  ...
)

# S3 method for class 'confint_spm'
plot(x, estimator = "all", ndec = 2, ...)

# S3 method for class 'confint_spm'
print(x, ...)

Arguments

object

An object of class c("spm", "exdex"), returned by spm.

parm

Specifies which parameter is to be given a confidence interval. Here there is only one option: the extremal index $\theta$.

level

A numeric scalar in (0, 1). The confidence level required.

maxima

A character scalar specifying whether to estimate confidence intervals based on sliding maxima or disjoint maxima.

interval_type

A character scalar: "norm" for intervals of type (a), "lik" for intervals of type (b).

conf_scale

A character scalar. If interval_type = "norm" then conf_scale determines the scale on which we use approximate large-sample normality of the estimators to estimate confidence intervals of type (a).

If conf_scale = "theta" then confidence intervals are estimated for $\theta$ directly. If conf_scale = "log" then confidence intervals are first estimated for $\log\theta$ and then transformed back to the $\theta$-scale.

Any bias-adjustment requested in the original call to spm, using it's bias_adjust argument, is automatically applied here.

constrain

A logical scalar. If constrain = TRUE then any confidence limits that are greater than 1 are set to 1, that is, they are constrained to lie in (0, 1]. Otherwise, limits that are greater than 1 may be obtained. If constrain = TRUE then any lower confidence limits that are less than 0 are set to 0.

bias_adjust

A logical scalar. If bias_adjust = TRUE then, if appropriate, bias-adjustment is also applied to the loglikelihood before it is adjusted using adjust_loglik. This is performed only if, in the call to spm, bias_adjust = "BB3" or "BB1" was specified, that is, we have object$bias_adjust = "BB3" or "BB1". In these cases the relevant component of object$bias_sl or object$bias_dj is used to scale $\theta$ so that the location of the maximum of the loglikelihood lies at the bias-adjusted estimate of $\theta$.

If bias_adjust = FALSE or object$bias_adjust = "none" or "N" then no bias-adjustment of the intervals is performed. In the latter case this is because the bias-adjustment is applied in the creation of the data in object$N2015_data and object$BB2018_data, on which the naive likelihood is based.

type

A character scalar. The argument type to be passed to conf_intervals in the chandwich package in order to estimate the likelihood-based intervals. Using type = "none" is not advised because then the intervals are based on naive estimated standard errors. In particular, if (the default) sliding = TRUE was used in the call to spm then the unadjusted likelihood-based confidence intervals provide vast underestimates of uncertainty.

...

Additional optional arguments to be passed to print.default

x

an object of class c("confint_spm", "exdex"), a result of a call to confint.spm.

estimator

A character vector specifying which of the three variants of the semiparametric maxima estimator to include in the plot: "N2015", "BB2018" or "BB2018b". See spm for details. If estimator = "all" then all three are included.

ndec

An integer scalar. The legend (if included on the plot) contains the confidence limits rounded to ndec decimal places.

Value

A list of class c("confint_spm", "exdex") containing the following components.

cis: A matrix with columns giving the lower and upper confidence limits. These are labelled as (1 - level)/2 and 1 - (1 - level)/2 in % (by default 2.5% and 97.5%). The row names are a concatenation of the variant of the estimator (N2015 for Northrop (2015), BB2018 for Berghaus and Bucher (2018)), BB2018b for the modified (by subtracting 1 / b) Berghaus and Bucher (2018) and the type of interval (norm for symmetric and lik for likelihood-based).
ciN: The object returned from conf_intervals that contains information about the adjusted loglikelihood for the Northrop (2015) variant of the estimator.
ciBB: The object returned from conf_intervals that contains information about the adjusted loglikelihood for the Berghaus and Bucher (2018) variant of the estimator.
ciBBb: The object returned from conf_intervals that contains information about the adjusted loglikelihood for the modified Berghaus and Bucher (2018) variant of the estimator.
call: The call to spm.
object: The input object.
maxima: The input maxima.
theta: The relevant estimates of $\theta$ returned from adjust_loglik. These are equal to object$theta_sl if maxima = "sliding", object$theta_dj if maxima = "disjoint", which provides a check that the results are correct.
level: The input level.

plot.confint_spm: nothing is returned.

print.confint_spm: the argument x, invisibly.

Details

The likelihood-based intervals are estimated using the adjust_loglik function in the chandwich package, followed by a call to conf_intervals. This adjusts the naive (pseudo-)loglikelihood so that the curvature of the adjust loglikelihood agrees with the estimated standard errors of the estimators. The option type = "none" should not be used in practice because the resulting confidence intervals will be wrong. In particular, in the intervals based on sliding maxima will provide vast underestimates of uncertainty.

If object$se contains NAs, because the block size b was too small or too large in the call to spm then confidence intervals cannot be estimated. A matrix of NAs will be returned. See the Details section of the spm documentation for more information.

print.confint_spm prints the matrix of confidence intervals for $\theta$.

References

Northrop, P. J. (2015) An efficient semiparametric maxima estimator of the extremal index. Extremes 18(4), 585-603. doi:10.1007/s10687-015-0221-5

Berghaus, B., Bucher, A. (2018) Weak convergence of a pseudo maximum likelihood estimator for the extremal index. Ann. Statist. 46(5), 2307-2335. doi:10.1214/17-AOS1621

Examples

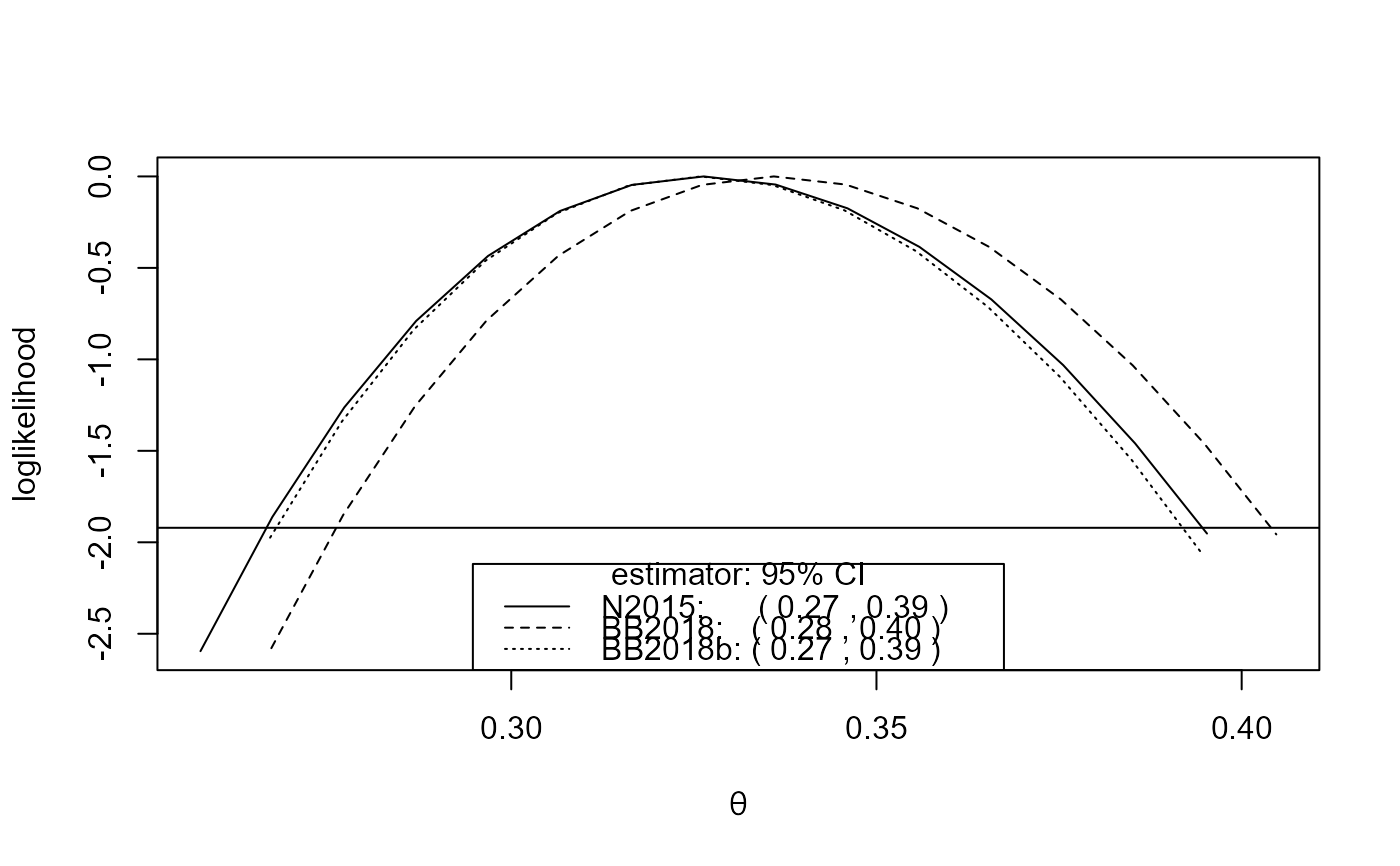
# Newlyn sea surges
theta <- spm(newlyn, 20)
confint(theta)
#>                 2.5 %    97.5 %
#> N2015norm   0.2002191 0.2782277
#> BB2018norm  0.2756477 0.3399961
#> BB2018bnorm 0.2256477 0.2899961
cis <- confint(theta, interval_type = "lik")
cis
#>                2.5 %    97.5 %
#> N2015lik   0.2028802 0.2797593
#> BB2018lik  0.2771474 0.3407445
#> BB2018blik 0.2321583 0.2853566
plot(cis)


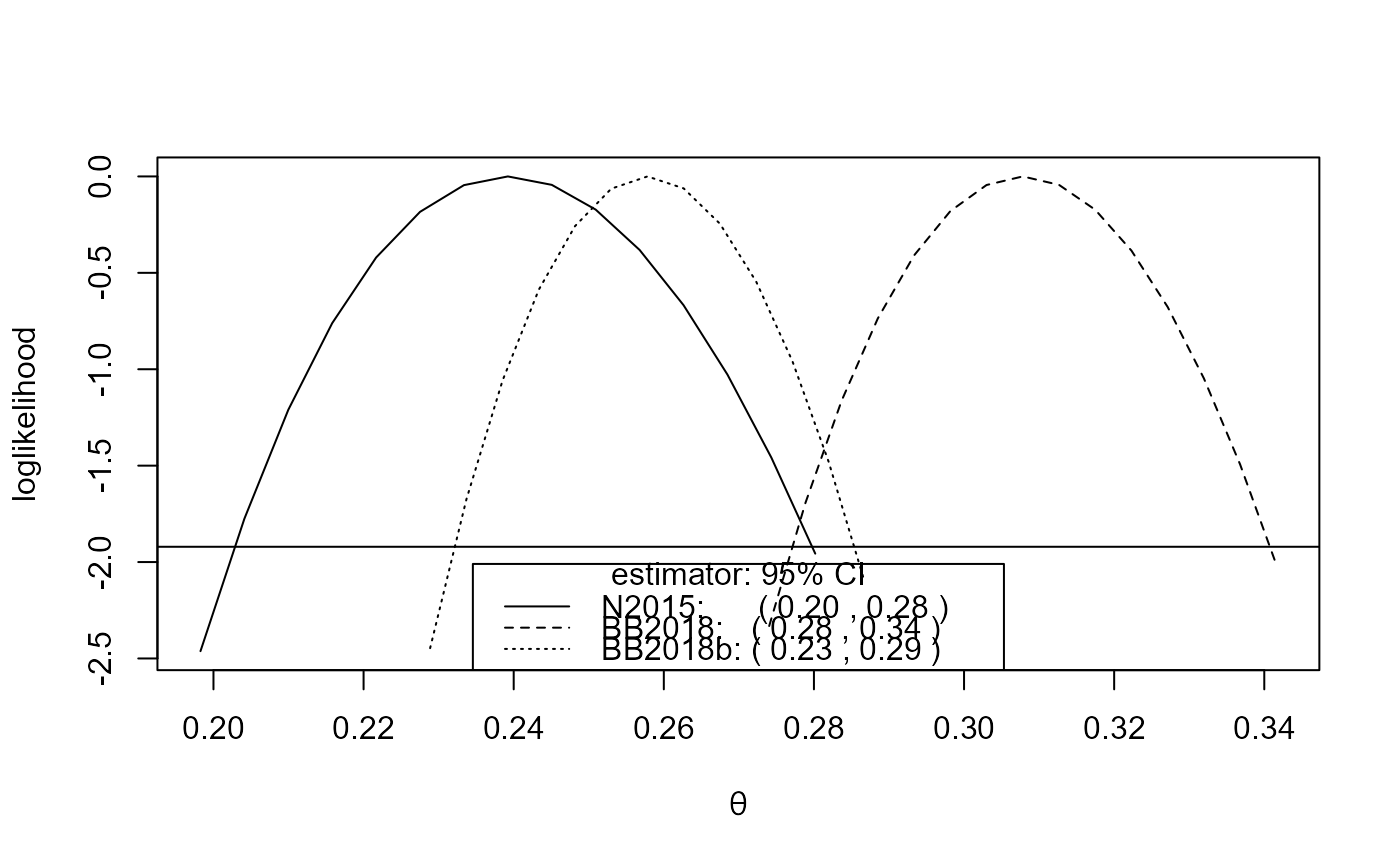# S&P 500 index
theta <- spm(sp500, 100)
confint(theta)
#>                 2.5 %    97.5 %
#> N2015norm   0.2607322 0.3919727
#> BB2018norm  0.2704307 0.4014686
#> BB2018bnorm 0.2604307 0.3914686
cis <- confint(theta, interval_type = "lik")
cis
#>                2.5 %    97.5 %
#> N2015lik   0.2664968 0.3946247
#> BB2018lik  0.2760426 0.4040249
#> BB2018blik 0.2678191 0.3919123
plot(cis)

Confidence intervals for the extremal index \(\theta\) for `"spm"` objects

Usage

Arguments

Value

Details

References

See also

Examples

Confidence intervals for the extremal index \(\theta\) for "spm" objects

Usage

Arguments

Value

Details

References

See also

Examples

Confidence intervals for the extremal index \(\theta\) for `"spm"` objects