The ITP root-finding algorithm

Performs one-dimensional root-finding using the ITP algorithm of Oliveira and Takahashi (2021). The function itp searches an interval [\(a\), \(b\)] for a root (i.e., a zero) of the function f with respect to its first argument. Each iteration results in a bracketing interval for the root that is narrower than the previous interval. If the function is discontinuous then a point of discontinuity at which the function changes sign may be found.

itp(
  f,
  interval,
  ...,
  a = min(interval),
  b = max(interval),
  f.a = f(a, ...),
  f.b = f(b, ...),
  epsilon = 1e-10,
  k1 = 0.2/(b - a),
  k2 = 2,
  n0 = 1
)

Arguments

f: An R function or an external pointer to a C++ function. For the latter see the article Passing user-supplied C++ functions in the Rcpp Gallery. The function for which the root is sought.
interval: A numeric vector c(a, b) of length 2 containing the end points of the interval to be searched for the root. The function values at the end points must be of opposite signs.
...: Additional arguments to be passed to f.
a, b: An alternative way to set the lower and upper end points of the interval to be searched. The function values at these end points must be of opposite signs.
f.a, f.b: The values of f(a) and f(b), respectively.
epsilon: A positive numeric scalar. The desired accuracy of the root. The algorithm continues until the width of the bracketing interval for the root is less than or equal to 2 * epsilon.
k1, k2, n0: Numeric scalars. The values of the tuning parameters \(\kappa\)₁, \(\kappa\)₂, \(n\)₀. See Details.

Value

An object (a list) of class "itp" containing the following components:

root: the location of the root, calculated as (a+b)/2, where [a, b] is the bracketing interval after convergence.
f.root: the value of the function evaluated at root.
iter: the number of iterations performed.
a,b: the end points of the bracketing interval [a, b] after convergence.
f.a,f.b: the values of function at a and b after convergence.
estim.prec: an approximate estimated precision for root, equal to the half the width of the final bracket for the root.

the root occurs at one of the input endpoints a or b then

iter = 0 and estim.prec = NA.

The returned object also has the attributes f (the input R function or pointer to a C++ function f), f_args (a list of additional arguments to f provided in ...), f_name

(a function name extracted from as.character(substitute(f)) or the form of the R function if f was not named), used_c (a logical scalar: FALSE, if f is an R function and TRUE

if f is a pointer to a C++ function) and input_a and

input_b (the input values of a and b). These attributes are used in plot.itp to produce a plot of the function f over the interval (input_a, input_b).

Details

Page 8 of Oliveira and Takahashi (2021) describes the ITP algorithm and the roles of the tuning parameters \(\kappa\)₁, \(\kappa\)₂ and \(n\)₀. The algorithm is described using pseudocode. The Wikipedia entry for the ITP method provides a summary. If the input function f is continuous over the interval [a, b] then the value of f evaluated at the estimated root is (approximately) equal to 0. If f is discontinuous over the interval [a, b] then the bracketing interval returned after convergence has the property that the signs of the function f at the end points of this interval are different and therefore the estimated root may be a point of discontinuity at which the sign of f changes.

The ITP method requires at most \(n\)_max = \(n\)_1/2 + \(n\)₀ iterations, where \(n\)_1/2 is the smallest integer not less than log₂((b-a) / 2\(\epsilon\)). If \(n\)₀ = 0 then the ITP method will require no more iterations than the bisection method. Depending on the function f, setting a larger value for \(n\)₀, e.g. the default setting \(n\)₀=1 used by the itp function, may result in a smaller number of iterations.

The default values of the other tuning parameters (epsilon = 1e-10, k1 = 0.2 / (b - a), k2 = 2) are set based on arguments made in Oliveira and Takahashi (2021).

References

Oliveira, I. F. D. and Takahashi, R. H. C. (2021). An Enhancement of the Bisection Method Average Performance Preserving Minmax Optimality, ACM Transactions on Mathematical Software, 47(1), 1-24. doi:10.1145/3423597

Examples

#### ----- The example used in the Wikipedia entry for the ITP method

# Supplying an R function
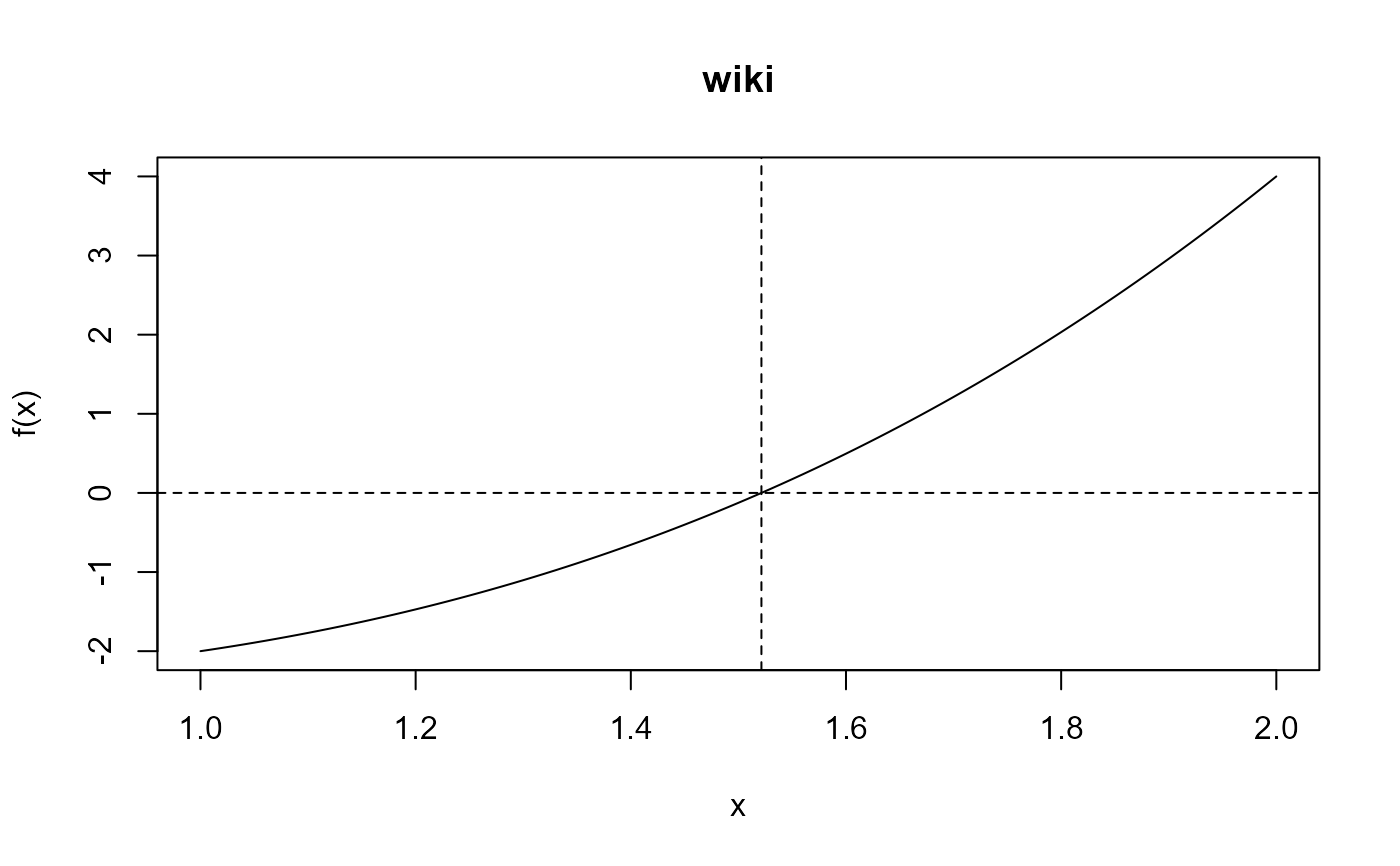
wiki <- function(x) x ^ 3 - x - 2
itp(wiki, c(1, 2), epsilon = 0.0005, k1 = 0.1, n0 = 1)
#> function: wiki 
#>       root     f(root)  iterations  
#>      1.521   7.698e-06           5  
# The default setting (with k1 = 0.2) wins by 1 iteration
wres <- itp(wiki, c(1, 2), epsilon = 0.0005, n0 = 1)
wres
#> function: wiki 
#>       root     f(root)  iterations  
#>      1.521   0.0001315           4  
plot(wres)


# Supplying an external pointer to a C++ function
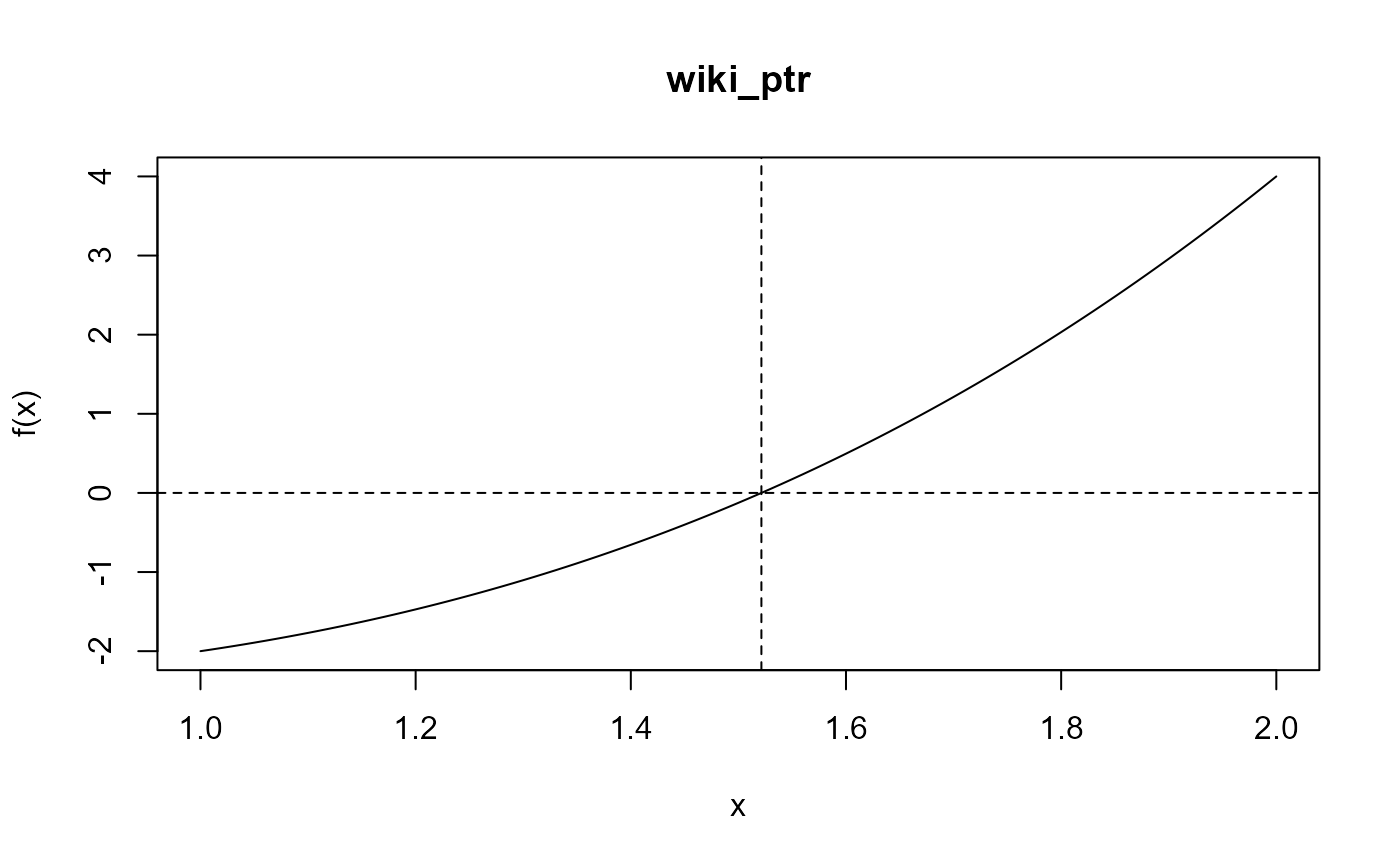
wiki_ptr <- xptr_create("wiki")
wres_c <- itp(f = wiki_ptr, c(1, 2), epsilon = 0.0005, k1 = 0.1)
wres_c
#> function: wiki_ptr 
#>       root     f(root)  iterations  
#>      1.521   7.698e-06           5  
plot(wres_c)


#### ----- Some examples from Table 1 of Oliveira and Takahashi (2021)

### Well-behaved functions

# Lambert
lambert <- function(x) x * exp(x) - 1
itp(lambert, c(-1, 1))
#> function: lambert 
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8  

# Trigonometric 1
# Supplying an R function
trig1 <- function(x, root) tan(x - root)
itp(trig1, c(-1, 1), root = 1 / 10)
#> function: trig1 
#>       root     f(root)  iterations  
#>        0.1  -8.238e-14           8  
# Supplying an external pointer to a C++ function
trig1_ptr <- xptr_create("trig1")
itp(f = trig1_ptr, c(-1, 1), root = 1 / 10)
#> function: trig1_ptr 
#>       root     f(root)  iterations  
#>        0.1  -8.238e-14           8  

# Logarithmic
logarithmic <- function(x, shift) log(abs(x - shift))
itp(logarithmic, c(-1, 1), shift = 10 /9)
#> function: logarithmic 
#>       root     f(root)  iterations  
#>     0.1111   8.991e-13           7  

# Linear
linear <- function(x) x
# Solution in one iteration
itp(linear, c(-1, 1))
#> function: linear 
#>       root     f(root)  iterations  
#>          0           0           1  
# Solution at an input endpoint
itp(linear, c(-1, 0))
#> function: linear 
#>       root     f(root)  iterations  
#>          0           0           0  

### Ill-behaved functions

## Non-simple zero

# Polynomial 3
poly3 <- function(x) (x * 1e6 - 1) ^ 3
itp(poly3, c(-1, 1))
#> function: poly3 
#>       root     f(root)  iterations  
#>      1e-06   -1.25e-13          36  
# Using n0 = 0 leads to fewer iterations, in this example
poly3 <- function(x) (x * 1e6 - 1) ^ 3
itp(poly3, c(-1, 1), n0 = 0)
#> function: poly3 
#>       root     f(root)  iterations  
#>      1e-06  -6.739e-14          35  

## Discontinuous

# Staircase
staircase <- function(x) ceiling(10 * x - 1) + 1 / 2
itp(staircase, c(-1, 1))
#> function: staircase 
#>       root     f(root)  iterations  
#>  7.404e-11         0.5          31  

## Multiple roots

# Warsaw
warsaw <- function(x) ifelse(x > -1, sin(1 / (x + 1)), -1)
# Function increasing over the interval
itp(warsaw, c(-1, 1))
#> function: warsaw 
#>       root     f(root)  iterations  
#>    -0.6817  -5.472e-11          11  
# Function decreasing over the interval
itp(warsaw, c(-0.85, -0.8))
#> function: warsaw 
#>       root     f(root)  iterations  
#>    -0.8408   6.494e-11           8