The Interpolate, Truncate, Project (ITP) Root-Finding Algorithm

The itp package implements the Interpolate, Truncate, Project (ITP) root-finding algorithm of Oliveira and Takahashi (2021). Each iteration of the algorithm results in a bracketing interval for the root that is narrower than the previous interval. It’s performance compares favourably with existing methods on both well-behaved functions and ill-behaved functions while retaining the worst-case reliability of the bisection method. For details see the authors’ Kudos summary and the Wikipedia article ITP method.

Examples

We use three examples from Section 3 of Oliveira and Takahashi (2021) to illustrate the use of the itp function. Each of these functions has a root in the interval $(-1, 1)$ . The function can be supplied either as an R function or as an external pointer to a C++ function.

library(itp)

A continuous function

The Lambert function $l(x) = xe^x - 1$ is continuous.

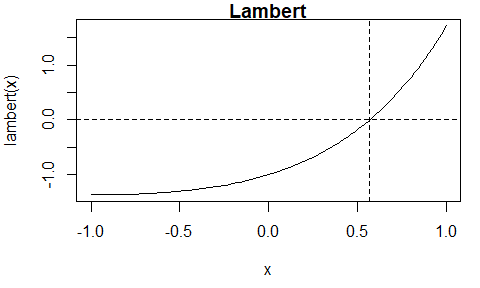
The itp function finds an estimate of the root, that is, $x^*$ for which $f(x^*)$ is (approximately) equal to 0. The algorithm continues until the length of the interval that brackets the root is smaller than $2 \epsilon$ , where $\epsilon$ is a user-supplied tolerance. The default is $\epsilon = 10^{-10}$ .

First, we supply an R function that evaluates the Lambert function.

# Lambert, using an R function
lambert <- function(x) x * exp(x) - 1
itp(lambert, c(-1, 1))
#> function: lambert 
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8

Now, we create an external pointer to a C++ function that has been provided in the itp package and pass this pointer to the function itp(). For more information see the Overview of the itp package vignette.

# Lambert, using an external pointer to a C++ function
lambert_ptr <- xptr_create("lambert")
itp(lambert_ptr, c(-1, 1))
#> function: lambert_ptr 
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8

The function `itp_c`

Also provided is the function itp_c, which is equivalent to itp, but the calculations are performed entirely using C++, and the arguments differ slightly: itp_c has a named required argument pars rather than ... and it does not have the arguments interval, f.a or f.b.

# Calling itp_c()
res <- itp_c(lambert_ptr, pars = list(), a = -1, b = 1)
res
#> function:  
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8

A discontinuous function

The staircase function $s(x) = \lceil 10 x - 1 \rceil + 1/2$ is discontinuous.

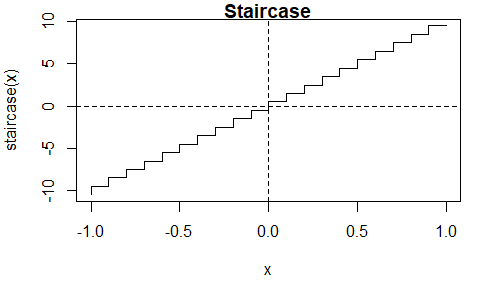
The itp function finds the discontinuity at $x = 0$ at which the sign of the function changes. The value of 0.5 returned for the root res$root is the midpoint of the bracketing interval [res$a, res$b] at convergence.

# Staircase
staircase <- function(x) ceiling(10 * x - 1) + 1 / 2
res <- itp(staircase, c(-1, 1))
print(res, all = TRUE)
#> function: staircase 
#>       root     f(root)  iterations           a           b         f.a  
#>  7.404e-11         0.5          31           0   1.481e-10        -0.5  
#>        f.b   precision  
#>        0.5   7.404e-11

A function with multiple roots

The Warsaw function $w(x) = I(x > -1)\left(1 + \sin\left(\frac{1}{1+x}\right)\right)-1$ has multiple roots.

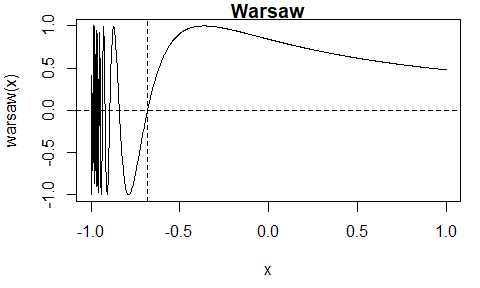
When the initial interval is $[-1, 1]$ the itp function finds the root $x \approx -0.6817$ . There are other roots that could be found from a different initial interval.

# Warsaw
warsaw <- function(x) ifelse(x > -1, sin(1 / (x + 1)), -1)
itp(warsaw, c(-1, 1))
#> function: warsaw 
#>       root     f(root)  iterations  
#>    -0.6817  -5.472e-11          11