Overview of the itp package

The Interpolate, Truncate, Project (ITP) root-finding algorithm was developed in Oliveira and Takahashi (2020). It’s performance compares favourably with existing methods on both well-behaved functions and ill-behaved functions while retaining the worst-case reliability of the bisection method. For details see the authors’ Kudos summary and the Wikipedia article ITP method.

The itp function implements the ITP method to find a root \(x^*\) of the function \(f: \mathbb{R} \rightarrow \mathbb{R}\) in the interval \([a, b]\), where \(f(a)f(b) < 0\). If \(f\) is continuous over \([a, b]\) then \(f(x^*) = 0\). If \(f\) is discontinuous over \([a, b]\) then \(x^*\) may be an estimate of a point of discontinuity at which the sign of \(f\) changes, that is, \(f(x^* - \delta)f(x^* + \delta) \leq 0\), where \(0 \leq \delta \leq \epsilon\) for some tolerance value \(\epsilon\).

We use some of the examples presented in Table 1 of Oliveira and Takahashi (2020) to illustrate the use of this function and run the examples using the uniroot function in the stats package as a means of comparison, using a convergence tolerance of \(10^{-10}\) in both cases. The itp function uses the following default values of the tuning parameters: \(\kappa_1 = 0.2 / (b - a)\), \(\kappa_2 = 2\) and \(n_0 = 1\), but these may be changed by the user. See Sections 2 and 3 of Oliveira and Takahashi (2020) for information. The following function prints output from uniroot in the same style as the output from itp.

# Method to print part of uniroot output
print.list <- function(x, digits = max(3L, getOption("digits") - 3L)) {
  names(x)[1:3] <- c("root", "f(root)", "iterations")
  print.default(format(x[1:3], digits = digits), print.gap = 2L, quote = FALSE)
}

library(itp)

First, we consider supplying the argument f to itp using an R function. Then we show how to supply an external pointer to a C++ function. For the simple examples given in the itp package only a modest improvement in speed is observed (and expected). However, being able to call itp() on the C++ side may have benefits in more challenging problems.

Supplying to `itp` an R function

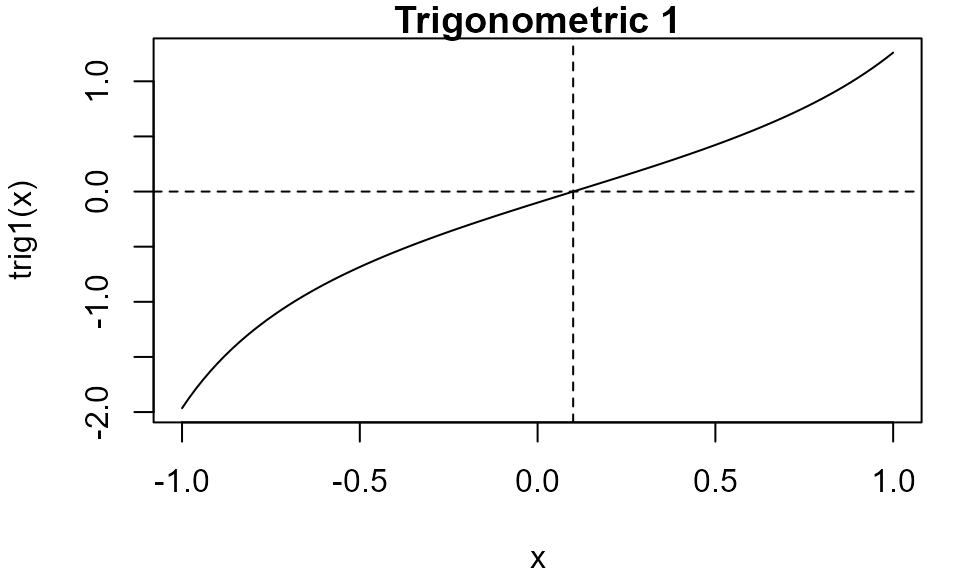
Well-behaved functions

These functions are infinitely differentiable and contain only one simple root over \([−1, 1]\).

Lambert: \(f(x) = x e^x - 1\)

# Lambert
lambert <- function(x) x * exp(x) - 1
itp(lambert, c(-1, 1))
#> function: lambert 
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8

uniroot(lambert, c(-1, 1), tol = 1e-10)
#>       root     f(root)  iterations  
#>     0.5671  -8.623e-12           8

Trigonometric 1: \(f(x) = \tan(x - 1 / 10)\)

# Trigonometric 1
trig1 <- function(x) tan(x - 1 /10)
itp(trig1, c(-1, 1))
#> function: trig1 
#>       root     f(root)  iterations  
#>        0.1  -8.238e-14           8

uniroot(trig1, c(-1, 1), tol = 1e-10)
#>       root     f(root)  iterations  
#>        0.1   6.212e-14           8

Ill-behaved functions

Polynomial 3 (non-simple root): \(f(x) = (10^6 x - 1) ^ 3\)

This function has a non-simple root at \(10^{-6}\), with a multiplicity of 3.

# Polynomial 3
poly3 <- function(x) (x * 1e6 - 1) ^ 3
itp(poly3, c(-1, 1))
#> function: poly3 
#>       root     f(root)  iterations  
#>      1e-06   -1.25e-13          36

# Using n0 = 0 leads to (slightly) fewer iterations, in this example
poly3 <- function(x) (x * 1e6 - 1) ^ 3
itp(poly3, c(-1, 1), n0 = 0)
#> function: poly3 
#>       root     f(root)  iterations  
#>      1e-06  -6.739e-14          35

uniroot(poly3, c(-1, 1), tol = 1e-10)
#>       root     f(root)  iterations  
#>      1e-06   1.771e-17          65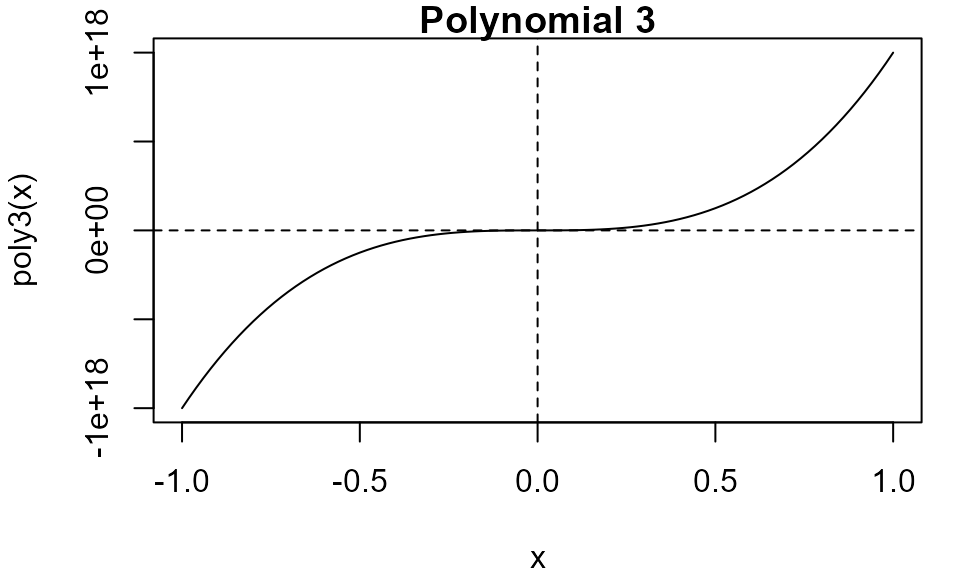

Staircase (discontinuous): \(f(x) = \lceil 10 x - 1 \rceil + 1/2\)

This function has discontinuities, including one at the location of the root.

# Staircase
staircase <- function(x) ceiling(10 * x - 1) + 1 / 2
itp(staircase, c(-1, 1))
#> function: staircase 
#>       root     f(root)  iterations  
#>  7.404e-11         0.5          31

uniroot(staircase, c(-1, 1), tol = 1e-10)
#>       root     f(root)  iterations  
#> -3.739e-11        -0.5          31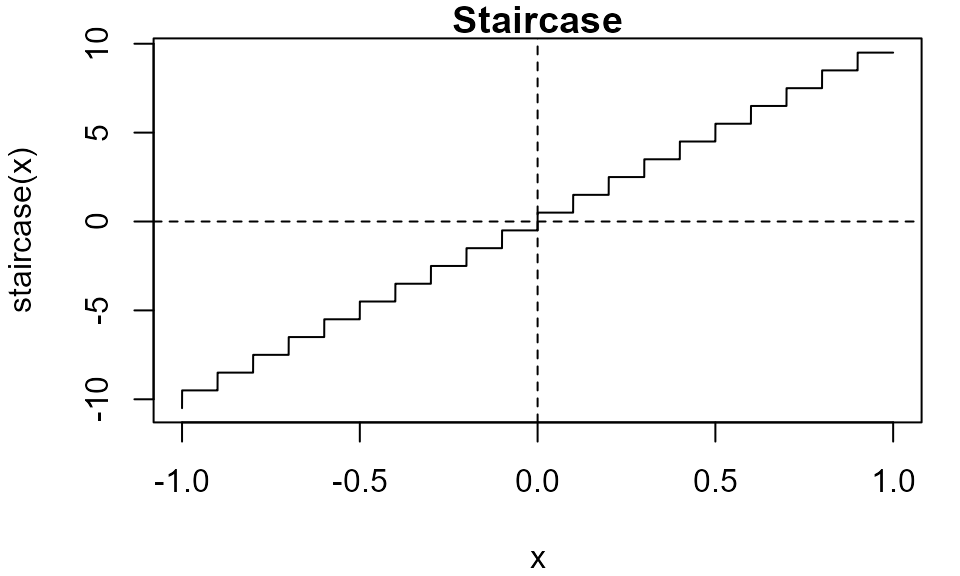

Warsaw (multiple roots): \(f(x) = I(x > -1)\left(1 + \sin\left(\frac{1}{1+x}\right)\right)-1\)

This function has multiple roots: we find two of them.

# Warsaw
warsaw <- function(x) ifelse(x > -1, sin(1 / (x + 1)), -1)
# Function increasing over the interval
itp(warsaw, c(-1, 1))
#> function: warsaw 
#>       root     f(root)  iterations  
#>    -0.6817  -5.472e-11          11

uniroot(warsaw, c(-1, 1), tol = 1e-10)
#>       root     f(root)  iterations  
#>    -0.6817  -3.216e-16           9

# Function decreasing over the interval
itp(warsaw, c(-0.85, -0.8))
#> function: warsaw 
#>       root     f(root)  iterations  
#>    -0.8408   6.494e-11           8

uniroot(warsaw, c(-0.85, -0.8), tol = 1e-10)
#>       root     f(root)  iterations  
#>    -0.8408  -3.021e-12           6

#> Warning in sin(1/(x + 1)): NaNs produced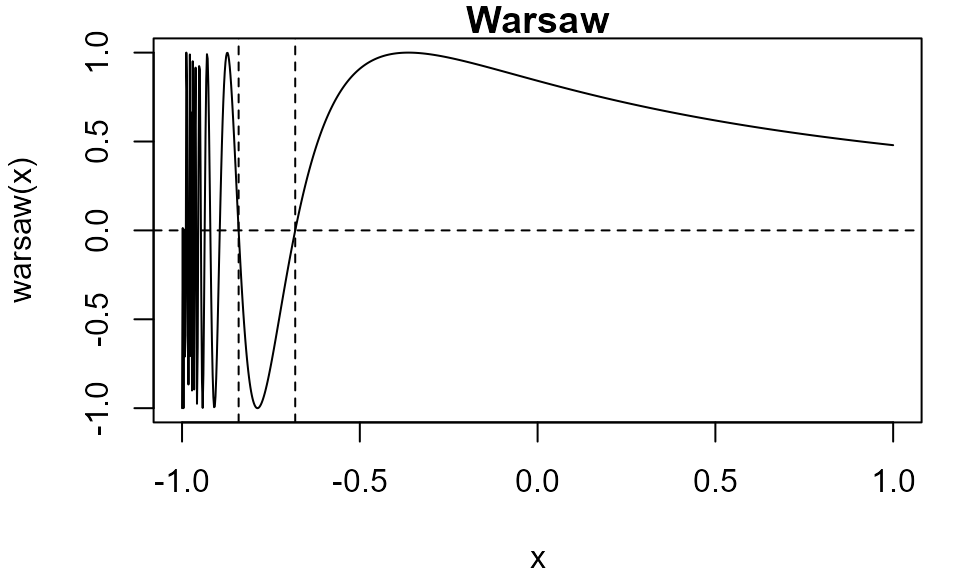

In terms of a naive comparison based on the number of iterations itp and uniroot perform similarly, except in the repeated-root “Polynomial 3” example, where itp requires fewer iterations.

Supplying to `itp` an external pointer to a C++ function

The general approach follows the article Passing user-supplied C++ functions in the Rcpp Gallery. The user writes a C++ function to calculate \(f\). This function must have a particular structure. As an example consider the following function, which implements the Lambert function considered above.

double lambert_cpp(const double& x, const List& pars) {
  return x * exp(x) - 1.0 ;
}

The function returns a value of double type and has two arguments: the first is the main argument and is of double type and the second is a list containing the values of additional parameters whose values are not specified inside the function. This list must be present, even if an empty list will be passed to the function. This allows the user to change the values of any parameters in \(f\) without editing the function.

One way to provide C++ functions is to create them in a file, say user_fns.cpp. Example content is provided below.

#include <Rcpp.h>
using namespace Rcpp;

// [[Rcpp::interfaces(r, cpp)]]

// User-supplied C++ functions for f.
// The only interface is double fun(const double& x, const List& pars).
// The second (List) argument must be included even if the function has no
// additional arguments.
// Each function must be prefaced by the line: // [[Rcpp::export]]

// [[Rcpp::export]]
double lambert_cpp(const double& x, const List& pars) {
  return x * exp(x) - 1.0 ;
}

// [[Rcpp::export]]
SEXP xptr_create(std::string fstr) {
  typedef double (*funcPtr)(const double& x, const List& pars) ;
  if (fstr == "lambert")
    return(XPtr<funcPtr>(new funcPtr(&lambert_cpp))) ;
  else
    return(XPtr<funcPtr>(R_NilValue)) ;
}

The full file is available on the itp Github page. The functions in this file are compiled and made available to R, either using the Rcpp::sourceCpp function (e.g. Rcpp::sourceCpp("user_fns.cpp")) or using RStudio’s Source button on the editor toolbar. The example content below also includes the function xptr_create, which creates an external pointer to a C++ function. It is this external pointer that is passed to itp. If the user has written a C++ function, say new_name, then they need to add to xptr_create (or their own version of this function) two lines of code:

else if (fstr == "new_name")  
  return(Rcpp::XPtr<funcPtr>(new funcPtr(&new_name))) ;

to create an external pointer for new_name using create_xptr.

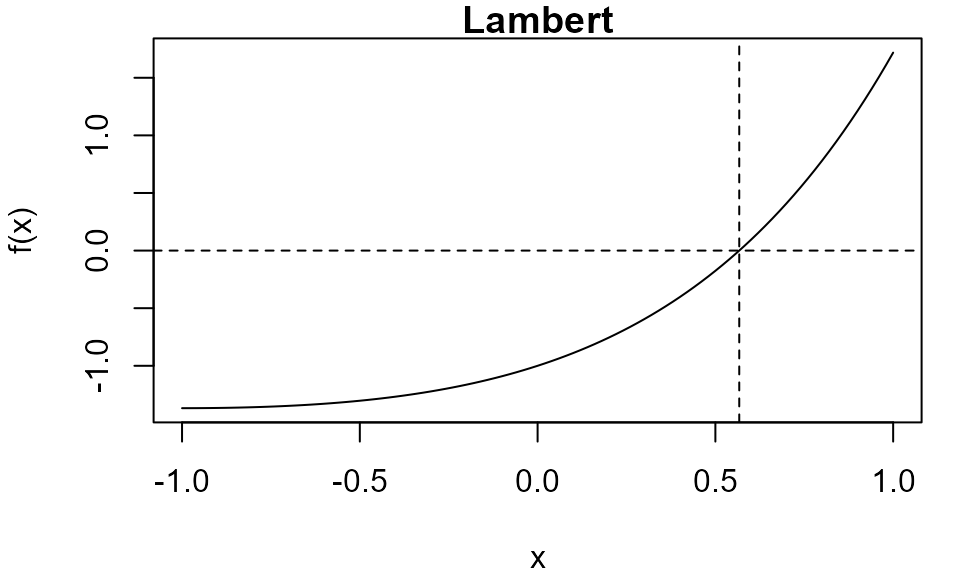
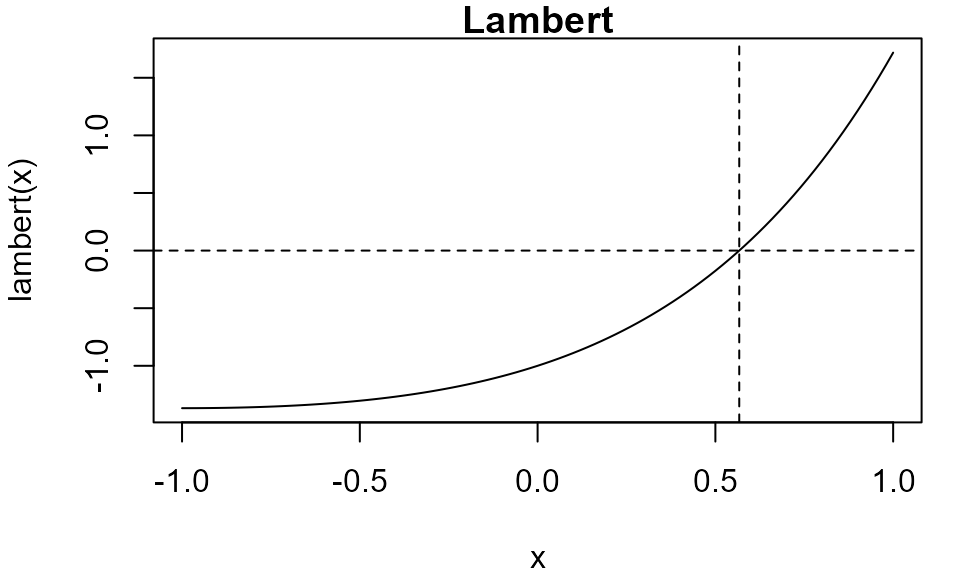
Lambert: \(f(x) = x e^x - 1\)

We repeat the Lambert example, obtaining the same results as above when we used an R function to supply the function.

# Lambert, using an external pointer to a C++ function
lambert_ptr <- xptr_create("lambert")
res <- itp(lambert_ptr, c(-1, 1))
res
#> function: lambert_ptr 
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8

C++ function `itp_c`

Also provided is the function itp_c, which is equivalent to itp, but the calculations are performed entirely using C++, and the arguments differ slightly: itp_c has a named required argument pars rather than ... and it does not have the arguments interval, f.a or f.b. This may be useful if you wish to call an ITP function on the C++ side.

# Calling itp_c()
res <- itp_c(lambert_ptr, pars = list(), a = -1, b = 1)
res
#> function:  
#>       root     f(root)  iterations  
#>     0.5671   2.048e-12           8

Plot method

Objects of class itp have a plot method that, by default, produces a plot of the function over the interval over which the root was sought and indicates the location of the root using dashed lines.

oldpar <- par(mar = c(4, 4, 1, 1))
plot(res, main = "Lambert")
par(oldpar)

References

Oliveira, I. F. D., and R. H. C. Takahashi. 2020. “An Enhancement of the Bisection Method Average Performance Preserving Minmax Optimality.” ACM Trans. Math. Softw. 47 (1). New York, NY, USA: Association for Computing Machinery. doi:10.1145/3423597.

Paul Northrop

2024-06-11

Supplying to `itp` an R function

Well-behaved functions

Lambert: \(f(x) = x e^x - 1\)

Trigonometric 1: \(f(x) = \tan(x - 1 / 10)\)

Ill-behaved functions

Polynomial 3 (non-simple root): \(f(x) = (10^6 x - 1) ^ 3\)

Staircase (discontinuous): \(f(x) = \lceil 10 x - 1 \rceil + 1/2\)

Warsaw (multiple roots): \(f(x) = I(x > -1)\left(1 + \sin\left(\frac{1}{1+x}\right)\right)-1\)

Supplying to `itp` an external pointer to a C++ function

Lambert: \(f(x) = x e^x - 1\)

C++ function `itp_c`

Plot method

References

Overview of the itp package

Paul Northrop

2024-06-11

Supplying to itp an R function

Well-behaved functions

Lambert: \(f(x) = x e^x - 1\)

Trigonometric 1: \(f(x) = \tan(x - 1 / 10)\)

Ill-behaved functions

Polynomial 3 (non-simple root): \(f(x) = (10^6 x - 1) ^ 3\)

Staircase (discontinuous): \(f(x) = \lceil 10 x - 1 \rceil + 1/2\)

Warsaw (multiple roots): \(f(x) = I(x > -1)\left(1 + \sin\left(\frac{1}{1+x}\right)\right)-1\)

Supplying to itp an external pointer to a C++ function

Lambert: \(f(x) = x e^x - 1\)

C++ function itp_c

Plot method

References

Supplying to `itp` an R function

Supplying to `itp` an external pointer to a C++ function

C++ function `itp_c`