The CRAN Task View on Extreme Value Analysis provides information about R packages that perform various extreme value analyses. The lax package supplements the functionality of nine of these packages, namely eva (Bader and Yan 2020), evd (Stephenson 2002), evir (Pfaff and McNeil 2018), extRemes (Gilleland and Katz 2016), fExtremes (Wuertz, Setz, and Yohan Chalabi 2017), ismev (Heffernan and Stephenson 2018), mev (Belzile et al. 2019), POT (Ribatet and Dutang 2016) and texmex (Southworth, Heffernan, and Metcalfe 2017). Univariate extreme value models, including regression models, are supported.
The chandwich package is used to provide robust sandwich estimation of parameter covariance matrix and loglikelihood adjustment for models fitted by maximum likelihood estimation. This may be useful for cluster correlated data when interest lies in the parameters of the marginal distributions, or for performing inferences that are robust to certain types of model misspecification.
lax works in an object-oriented way, operating on R objects
returned from functions in other packages that summarise the fit of an
extreme value model. Loglikelihood adjustment and sandwich estimation is
performed by an alogLik S3 method. We demonstrate this
using the following running example, which involves fitting a
Generalised Extreme Value (GEV) regression model. Firstly, we use the
ismev package to produce the fitted GEV regression model object
on which alogLik will operate, and illustrate what can be
done with the objects returned from alogLik. We use the
ismev package because it provides an example of a case where we
need to refit the model in order to obtain the information that we need
to perform adjusted inferences. Then we repeat the adjustment using
seven of the other eight packages. The POT package specialises
in Generalised Pareto (GP) modelling, for which we use a different
example.
GEV regression of annual maximum temperatures
This example is based on the analysis presented in Section 5.2 of
Chandler and Bate (2007). The data, which
are available in the data frame ow, are a bivariate time
series of annual maximum temperatures, recorded in degrees Fahrenheit,
at Oxford and Worthing in England, for the period 1901 to 1980. If
interest is only in the marginal distributions of high temperatures in
Oxford and Worthing, then we might fit a GEV regression model in which
some or all of the parameters may vary between Oxford and Worthing.
However, we should adjust for the cluster dependence between
temperatures recorded during the same year.
ismev
The gev.fit() function in ismev fits GEV
regression models. It allows covariate effects in any of the (location,
scale and shape) parameters of the GEV distribution. However, an object
returned from gev.fit() does not provide all the
information about a fitted regression model that alogLik
needs, in order to calculate loglikelihood contributions from individual
observations: the design matrices are missing. Therefore, lax
provides the function gev_refit, which is a version of
gev.fit that adds this information.
The following code fits a GEV regression model in which the location,
scale and shape parameters of the GEV distribution vary between Oxford
and Worthing. Then alogLik is used to provide adjusted
standard errors and an adjusted loglikelihood.
library(lax)
# Column 4 of ow contains 1 for Oxford and -1 for Worthing
large <- gev_refit(ow$temp, ow, mul = 4, sigl = 4, shl = 4, show = FALSE,
method = "BFGS")
# Adjust the loglikelihood and standard errors
adj_large <- alogLik(large, cluster = ow$year, cadjust = FALSE)
# MLEs, SEs and adjusted SEs
t(summary(adj_large))
#> loc locloc scale scaleloc shape shapeloc
#> MLE 81.1700 2.6690 3.7290 0.5312 -0.19890 -0.08835
#> SE 0.3282 0.3282 0.2292 0.2292 0.04937 0.04937
#> adj. SE 0.4036 0.2128 0.2425 0.1911 0.03944 0.03625This reproduces the values in rows 1, 3 and 4 in Table 2 of Chandler and Bate (2007). The estimation of the
‘meat’ of the sandwich adjustment is performed using the sandwich package.
In this example, we need to pass cadjust = FALSE to
sandwich::meatCL in order that the adjustment is the same
as that used in Chandler and Bate (2007).
Otherwise, meatCL makes a finite-cluster bias
correction.
Confidence intervals
A confint method calculates approximate (95%) confidence
intervals for the parameters, based on the adjusted loglikelihood. Chandler and Bate (2007) consider three types of
loglikelihood adjustment: one vertical and two horizontal. The type of
adjustment is selected by the argument type. The default is
type = "vertical" and there is an option to perform no
adjustment.
confint(adj_large)
#> Waiting for profiling to be done...
#> 2.5 % 97.5 %
#> loc 80.3729001 81.9602100
#> locloc 2.2437419 3.0831279
#> scale 3.2991896 4.2598984
#> scaleloc 0.1611912 0.9433844
#> shape -0.2741177 -0.1157069
#> shapeloc -0.1652089 -0.0200268
confint(adj_large, type = "none")
#> Waiting for profiling to be done...
#> 2.5 % 97.5 %
#> loc 80.52440863 81.813160870
#> locloc 2.01969229 3.308352990
#> scale 3.32435238 4.236272757
#> scaleloc 0.09100223 1.020139218
#> shape -0.28957175 -0.094326264
#> shapeloc -0.18850187 0.008628523Confidence regions
The conf_region function in the chandwich
package can be used to produce confidence regions for pairs of
parameters. Here, we consider the ‘central’ (midway between Oxford and
Worthing) scale and shape intercept parameters: \(\sigma_0\) and \(\xi_0\) in Chandler
and Bate (2007).
library(chandwich)
which_pars <- c("scale", "shape")
gev_none <- conf_region(adj_large, which_pars = which_pars, type = "none")
#> Waiting for profiling to be done...
gev_vertical <- conf_region(adj_large, which_pars = which_pars)
#> Waiting for profiling to be done...
plot(gev_none, gev_vertical, lwd = 2, xlim = c(3.1, 4.5), ylim = c(-0.35, -0.05),
xlab = expression(sigma[0]), ylab = expression(xi[0]))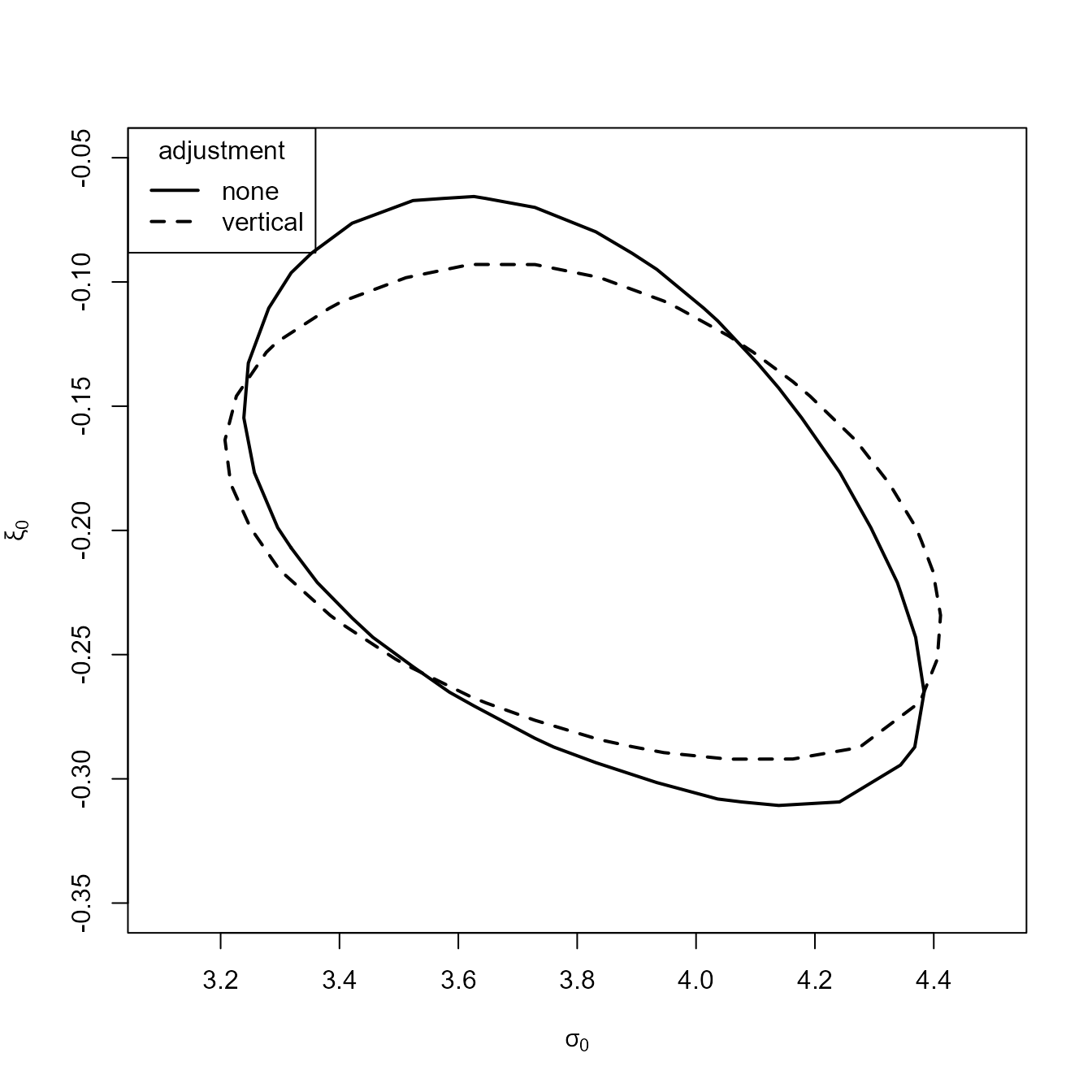
Comparing nested models
alogLik also has an anova method, which can
be used to perform (adjusted) loglikelihood ratio tests of nested
models. To illustrate this we fit, and adjust, a smaller model, in which
Oxford and Worthing have a common GEV shape parameter, and then compare
this model to the larger one.
small <- gev_refit(ow$temp, ow, mul = 4, sigl = 4, show = FALSE,
method = "BFGS")
adj_small <- alogLik(small, cluster = ow$year, cadjust = FALSE)
summary(adj_small)
#> MLE SE adj. SE
#> loc 81.1200 0.3260 0.40640
#> locloc 2.4540 0.3047 0.20370
#> scale 3.7230 0.2232 0.24020
#> scaleloc 0.3537 0.2096 0.16840
#> shape -0.1845 0.0488 0.04028
anova(adj_large, adj_small)
#> Analysis of (Adjusted) Deviance Table
#>
#> Model.Df Df ALRTS Pr(>ALRTS)
#> adj_large 6
#> adj_small 5 1 6.3572 0.01169 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(adj_large, adj_small, type = "none")
#> Analysis of (Adjusted) Deviance Table
#>
#> Model.Df Df ALRTS Pr(>ALRTS)
#> adj_large 6
#> adj_small 5 1 3.1876 0.0742 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We see that the adjustment of the loglikelihood for clustering makes enough of a difference to matter: if we perform a test at the 5% significance level then we choose the larger model when we adjust but the smaller model if we do not.
evd
The fgev() function in evd fits GEV regression
models, but it only allows covariate effects in the location
parameter.
extRemes
library(extRemes, quietly = TRUE)
fevd_fit <- fevd(temp, ow, location.fun = ~ ow$loc, scale.fun = ~ ow$loc,
shape.fun = ~ ow$loc)
adj_fevd_fit <- alogLik(fevd_fit, cluster = ow$year)
summary(adj_fevd_fit)
#> MLE SE adj. SE
#> mu0 81.17000 0.32820 0.40620
#> mu1 2.66800 0.32820 0.21420
#> sigma0 3.72900 0.22930 0.24410
#> sigma1 0.53090 0.22930 0.19230
#> xi0 -0.19890 0.04938 0.03969
#> xi1 -0.08828 0.04938 0.03648eva
library(eva, quietly = TRUE)
gevr_fit <- gevrFit(ow$temp, information = "observed",
locvars = ow, locform = ~ ow$loc,
scalevars = ow, scaleform = ~ ow$loc,
shapevars = ow, shapeform = ~ ow$loc)
adj_gevr_fit <- alogLik(gevr_fit, cluster = ow$year)
summary(adj_gevr_fit)
#> MLE SE adj. SE
#> Location (Intercept) 81.1700 0.32810 0.40620
#> Location ow$loc 2.6680 0.32810 0.21420
#> Scale (Intercept) 3.7290 0.22920 0.24400
#> Scale ow$loc 0.5307 0.22920 0.19230
#> Shape (Intercept) -0.1989 0.04936 0.03968
#> Shape ow$loc -0.0882 0.04936 0.03647evir
The gev() function in evir only fits stationary
GEV models.
fExtremes
The gevFit() function in fExtremes only fits
stationary GEV models.
mev
The fit.gev() function in mev only fits
stationary GEV models.
POT
Among other things, the fitgpd() function in the
POT package can fit a GP distribution to threshold excesses
using maximum likelihood estimation. We illustrate alogLik
using an example from the fitgpd documentation. There is no
cluster dependence here. However, there may be interest in using a
sandwich estimator of covariance if we are concerned about model
misspecification. In this case, where we simulate from the correct
model, we expect the adjustment to make little difference, and so it
proves.