Frequentist threshold-based inference for time series extremes

Performs threshold-based frequentist inference for 3 aspects of stationary time series extremes: the probability that the threshold is exceeded, the marginal distribution of threshold excesses and the extent of clustering of extremes, as summarised by the extremal index.

flite(data, u, cluster, k = 1, inc_cens = TRUE, ny, ...)

Arguments

data

A numeric vector or numeric matrix of raw data. If data is a matrix then the log-likelihood is constructed as the sum of (independent) contributions from different columns. A common situation is where each column relates to a different year.

If data contains missing values then split_by_NAs is used to divide the data further into sequences of non-missing values, stored in different columns in a matrix. Again, the log-likelihood is constructed as a sum of contributions from different columns.

u

A numeric scalar. The extreme value threshold applied to the data. See Details for information about choosing u.

cluster

This argument is used to set the argument cluster to meatCL, which calculates the matrix \(V\) passed as the argument V to adjust_loglik. If data is a matrix and cluster is missing then cluster is set so that data in different columns are in different clusters. If data is a vector and cluster is missing then cluster is set so that each observation forms its own cluster.

If cluster is supplied then it must have the same structure as data: if data is a matrix then cluster must be a matrix with the same dimensions as data and if data is a vector then cluster must be a vector of the same length as data. Each entry in cluster sets the cluster of the corresponding component of data.

k, inc_cens

Arguments passed to kgaps. k sets the value of the run parameter \(K\) in the \(K\)-gaps model for the extremal index. inc_cens determines whether contributions from right-censored inter-exceedance times are used. See Details for information about choosing k.

ny

A numeric scalar. The (mean) number of observations per year. Setting this appropriately is important when making inferences about return levels, using returnLevel, but ny is not used by flite so it need not be supplied now. If ny is supplied to flite then it is stored for use by returnLevel. Alternatively, ny can be supplied in a later call to returnLevel. If ny is supplied to both flite and returnLevel then the value supplied to returnLevel will take precedence, with no warning given.

...

Further arguments to be passed to the function meatCL in the sandwich package. In particular, the clustering adjustment argument cadjust may make a difference if the number of clusters is not large.

Value

An object of class c("flite", "lite", "chandwich"). This object is a function with 2 arguments:

pars, a numeric vector of length 4 to supply the value of the parameter vector (\(p\)_u, \(\sigma\)_u, \(\xi\), \(\theta\)),
type, a character scalar specifying the type of adjustment made to the independence log-likelihood in parts 1 and 2, one of "vertical", "none", "cholesky", or "spectral". For details see Chandler and Bate (2007). The default is "vertical" for the reason given in the description of the argument adj_type in plot.flite.

The object also has the attributes "Bernoulli", "gp",

"theta", which provide the fitted model objects returned from

adjust_loglik (for "Bernoulli" and

"gp") and kgaps (for "theta"). The named input arguments are returned in a list as the attribute

inputs. If ny was not supplied then its value is NA. The call to flite is provided in the attribute "call".

Objects inheriting from class "flite" have coef,

logLik, nobs, plot, summary, vcov

and confint methods. See fliteMethods.

returnLevel can be used to make frequentist inferences about return levels.

Details

There are 3 independent parts to the inference, all performed using maximum likelihood estimation.

A Bernoulli(\(p\)_u) model for whether a given observation exceeds the threshold \(u\).
A generalised Pareto, GP(\(\sigma\)_u, \(\xi\)), model for the marginal distribution of threshold excesses.
The \(K\)-gaps model for the extremal index \(\theta\).

The general approach follows Fawcett and Walshaw (2012).

For parts 1 and 2, inferences based on a mis-specified independence log-likelihood are adjusted to account for clustering in the data. Here, we follow Chandler and Bate (2007) to estimate adjusted log-likelihood functions for \(p\)_u and for (\(\sigma\)_u, \(\xi\)), with the argument cluster defining the clusters. This aspect of the calculations is performed using the adjust_loglik in the chandwich package (Northrop and Chandler, 2021). The GP distribution initial fit of the GP distribution to threshold excesses is performed using the grimshaw_gp_mle function in the revdbayes package (Northrop, 2020).

In part 3, the methodology described in Suveges and Davison (2010) is implemented using the exdex package (Northrop and Christodoulides, 2022).

Two tuning parameters need to be chosen: a threshold \(u\) and the \(K\)-gaps run parameter \(K\). The exdex package has a function choose_uk to inform this choice.

Each part of the inference produces a log-likelihood function (adjusted for parts 1 and 2). These log-likelihoods are combined (summed) to form a log-likelihood function for the parameter vector (\(p\)_u, \(\sigma\)_u, \(\xi\), \(\theta\)). Return levels are a function of these parameters and therefore inferences for return levels can be based on this log-likelihood.

References

Chandler, R. E. and Bate, S. (2007). Inference for clustered. data using the independence loglikelihood. Biometrika, 94(1), 167-183. doi:10.1093/biomet/asm015

Fawcett, L. and Walshaw, D. (2012), Estimating return levels from serially dependent extremes. Environmetrics, 23, 272-283. doi:10.1002/env.2133

Northrop, P. J. and Chandler, R. E. (2021). chandwich: Chandler-Bate Sandwich Loglikelihood Adjustment. R package version 1.1.5. https://CRAN.R-project.org/package=chandwich.

Northrop, P. J. and Christodoulides, C. (2022). exdex: Estimation of the Extremal Index. R package version 1.1.1. https://CRAN.R-project.org/package=exdex/.

Northrop, P. J. (2020). revdbayes: Ratio-of-Uniforms Sampling for Bayesian Extreme Value Analysis. R package version 1.3.9. https://paulnorthrop.github.io/revdbayes/

Suveges, M. and Davison, A. C. (2010) Model misspecification in peaks over threshold analysis, Annals of Applied Statistics, 4(1), 203-221. doi:10.1214/09-AOAS292

Examples

### Cheeseboro wind gusts

# Make inferences
cdata <- exdex::cheeseboro
# Each column of the matrix cdata corresponds to data from a different year
# flite() sets cluster automatically to correspond to column (year)
cfit <- flite(cdata, u = 45, k = 3)
summary(cfit)
#> 
#> Call:
#> flite(data = cdata, u = 45, k = 3)
#> 
#>          Estimate Std. Error
#> p[u]      0.02771   0.005988
#> sigma[u]  9.27400   2.071000
#> xi       -0.09368   0.084250
#> theta     0.24050   0.023360

# 2 ways to find the maximised log-likelihood value
cfit(coef(cfit))
#> [1] -1791.28
logLik(cfit)
#> 'log Lik.' -1791.28 (df=4)

# Plots of (adjusted) log-likelihoods
plot(cfit)
#> Waiting for profiling to be done...
#> Waiting for profiling to be done...
#> Waiting for profiling to be done...

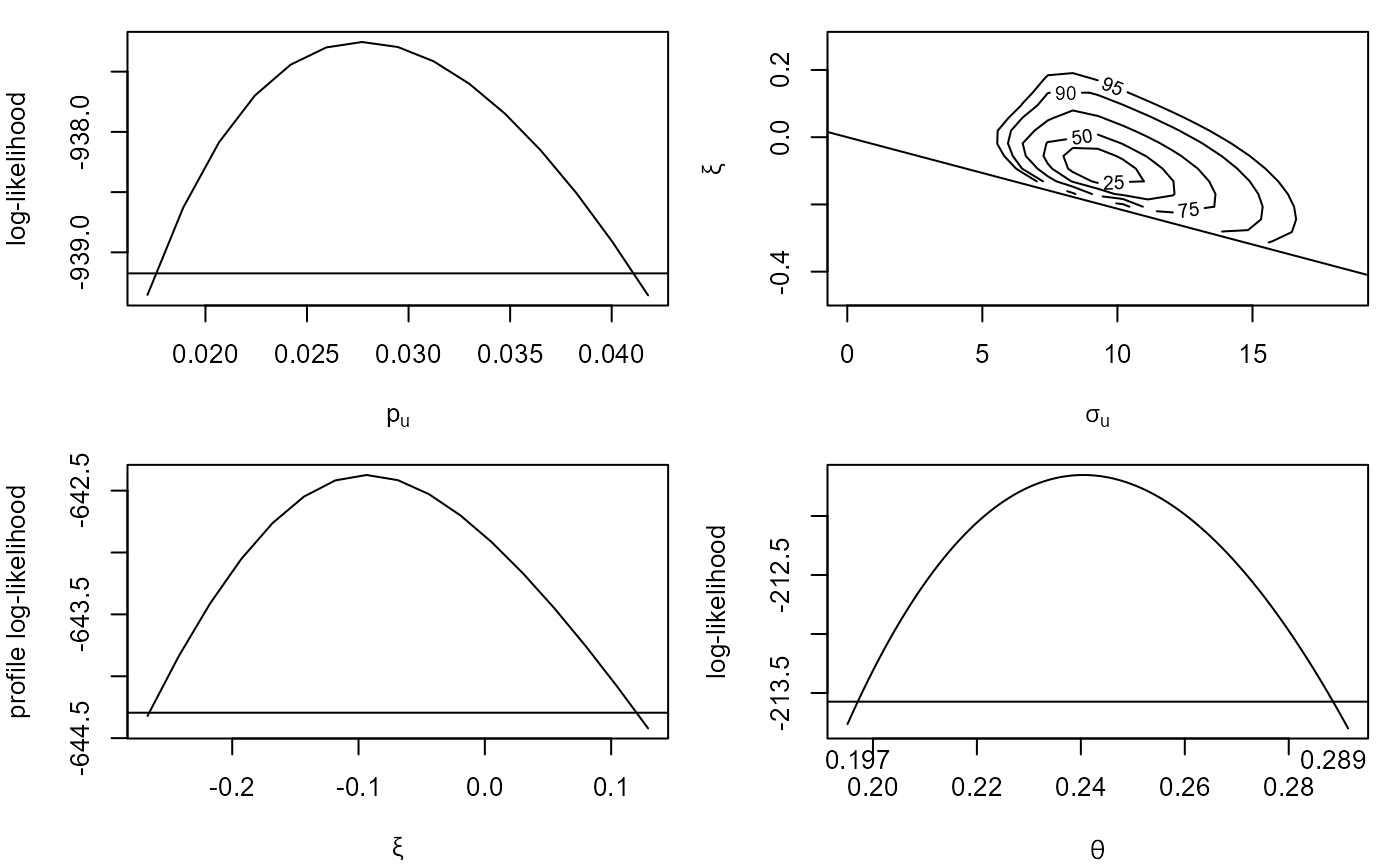plot(cfit, which = "gp")
#> Waiting for profiling to be done...


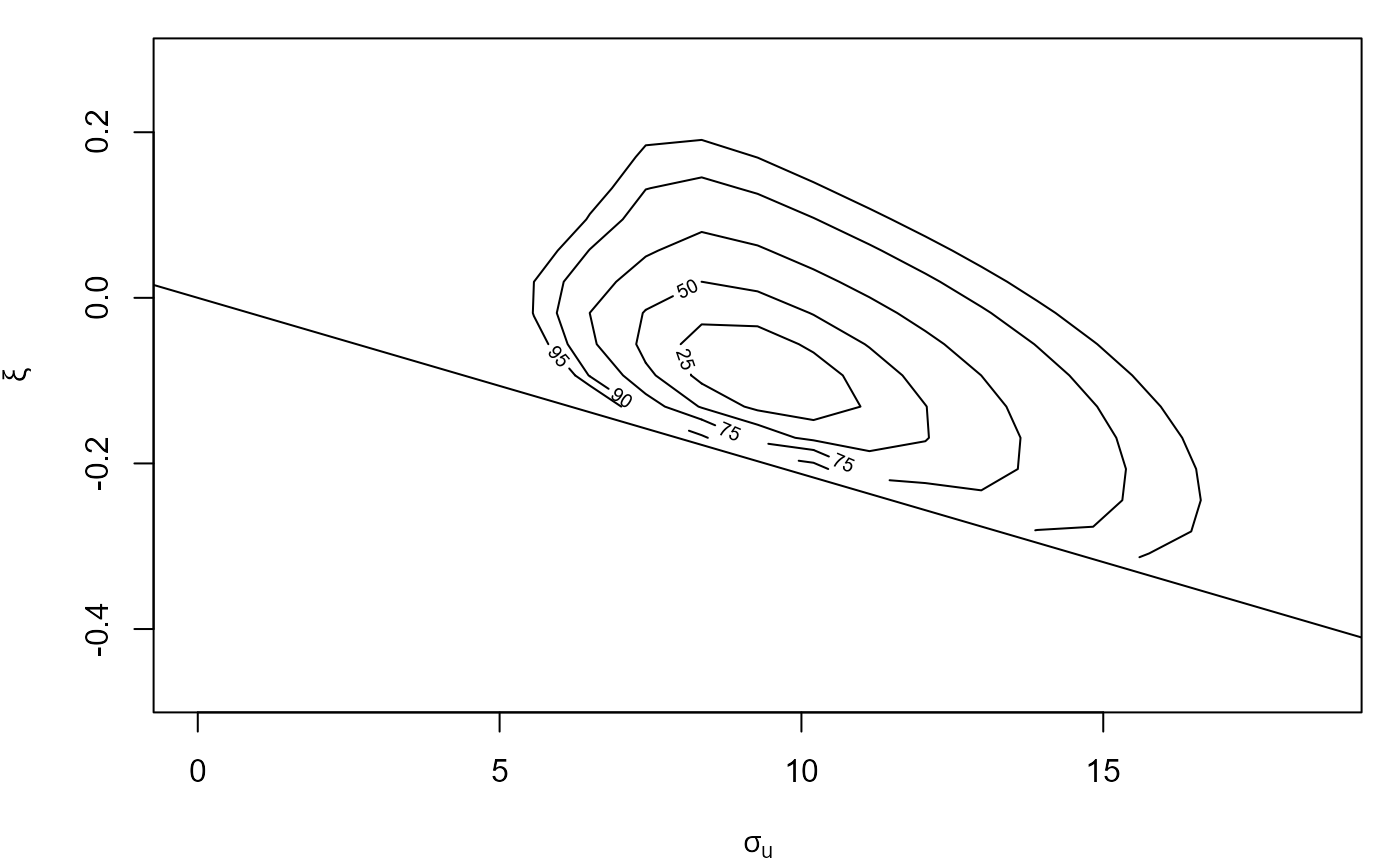## Confidence intervals
# Based on an adjusted profile log-likelihood
confint(cfit)
#> Waiting for profiling to be done...
#> Waiting for profiling to be done...
#> Waiting for profiling to be done...
#>               2.5%       97.5%
#> pu      0.01758135  0.04107051
#> sigmau  6.11637816 14.69866203
#> xi     -0.26574658  0.12007715
#> theta   0.19707488  0.28853513
# Symmetric intervals based on large sample normality
confint(cfit, profile = FALSE)
#>              2.5%       97.5%
#> pu      0.0159747  0.03944569
#> sigmau  5.2143559 13.33351127
#> xi     -0.2588087  0.07145532
#> theta   0.1946896  0.28627628