The ITP root-finding algorithm using C++

Performs one-dimensional root-finding using the ITP algorithm of Oliveira and Takahashi (2021). This function is equivalent to itp but calculations are performed entirely using C++, and the arguments differ slightly: itp_c has a named required argument pars rather than ... and it does not have the arguments interval, f.a or f.b.

itp_c(f, pars, a, b, epsilon = 1e-10, k1 = -1, k2 = 2, n0 = 1)

Arguments

f

An external pointer to a C++ function that evaluates the function \(f\).

pars

A list of additional arguments to the function. This may be an empty list.

a, b

Numeric scalars. Lower (a) and upper b limits of the interval to be searched for a root.

epsilon

A positive numeric scalar. The desired accuracy of the root. The algorithm continues until the width of the bracketing interval for the root is less than or equal to 2 * epsilon.

k1, k2, n0

Numeric scalars. The values of the tuning parameters \(\kappa\)₁, \(\kappa\)₂, \(n\)₀. See the Details section of itp.

The default value for k1 in itp_c is set as the inadmissible value of -1 (in reality \(\kappa\)₁ must be positive) as a device to set the same default value for k1 as itp, that is, k1 = 0.2 / (b - a). If the input value of k1 is less than or equal to 0 then, inside itp_c, k1 = 0.2 / (b - a) is set.

Value

An object (a list) of class "itp" with the same structure as detailed in the Value section of itp, except that the attribute f_name is empty (equal to "").

Details

For details see itp.

References

Oliveira, I. F. D. and Takahashi, R. H. C. (2021). An Enhancement of the Bisection Method Average Performance Preserving Minmax Optimality, ACM Transactions on Mathematical Software, 47(1), 1-24. doi:10.1145/3423597

Examples

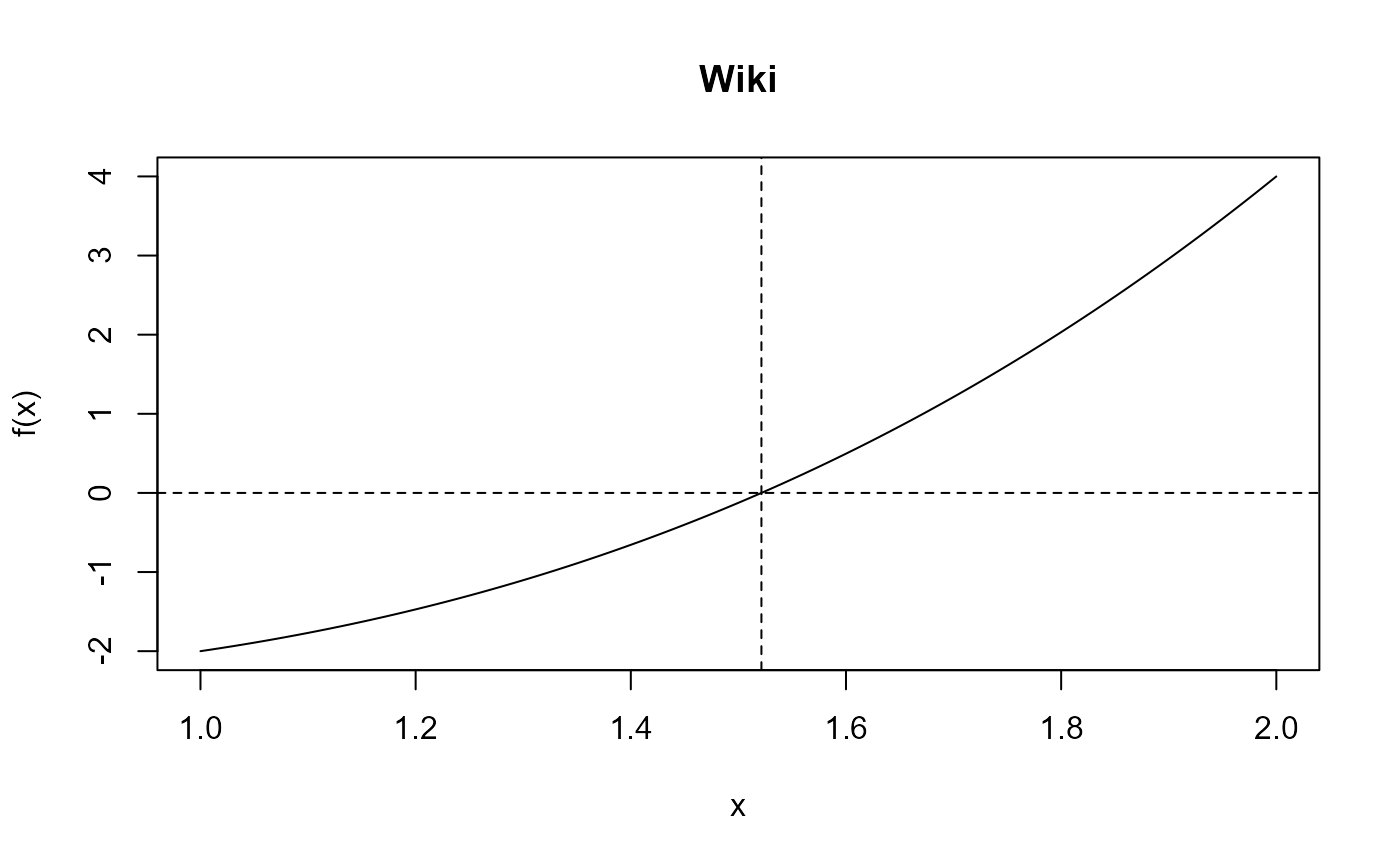
wiki_ptr <- xptr_create("wiki")
wres <- itp_c(f = wiki_ptr, pars = list(), a = 1, b = 2, epsilon = 0.0005)
wres
#> function:  
#>       root     f(root)  iterations  
#>      1.521   0.0001315           4  
plot(wres, main = "Wiki")