EVA 2021 R Workshop: revdbayes

How did revdbayes start?

I needed to sample quickly and automatically from many EV (generalised Pareto) posteriors
threshr: threshold selection based on
- out-of-sample EV predictions
- leave-one-out cross-validation
wanted to account for parameter uncertainty
wanted to avoid MCMC tuning and convergence diagnostics

What does revdbayes do?

Direct sampling from (simple) EV posterior distributions
Has similar functionality to evdbayes

	evdbayes	revdbayes
method	Markov chain Monte Carlo (MCMC)	ratio-of-uniforms (ROU)
tuning	required	largely automatic
sample	dependent	random
checking	yes	no

Ratio-of-uniforms method

\(d\)-dimensional continuous \(X = (X_1, \ldots, X_d)\) with density \(\propto\) \(f(x)\)

If \((u, v_1, \ldots, v_d)\) are uniformly distributed over

\[ C(r) = \left\{ (u, v_1, \ldots, v_d): 0 < u \leq \left[ f\left( \frac{v_1}{u^r}, \ldots, \frac{v_d}{u^r} \right) \right] ^ {1/(r d + 1)} \right\} \]

for some \(r \geq 0\), then \((v_1 / u ^r, \ldots, v_d / u ^ r)\) has density \(f(x) / \int f(x) {\rm ~d}x\)

Acceptance-rejection algorithm

simulate uniformly over a \((d+1)\)-dimensional bounding box \(\{ 0 < u \leq a(r), \, b_i^-(r) \leq v_i \leq b_i^+(r), \, i = 1, \ldots, d \}\)
if simulated \((u, v_1, \ldots, v_d) \in C(r)\) then accept \(x = (v_1 / u ^r, \ldots, v_d / u ^ r)\)

Limitations

\(f\) must be bounded
\(C(r)\) must be ‘boxable’

Increasing efficiency

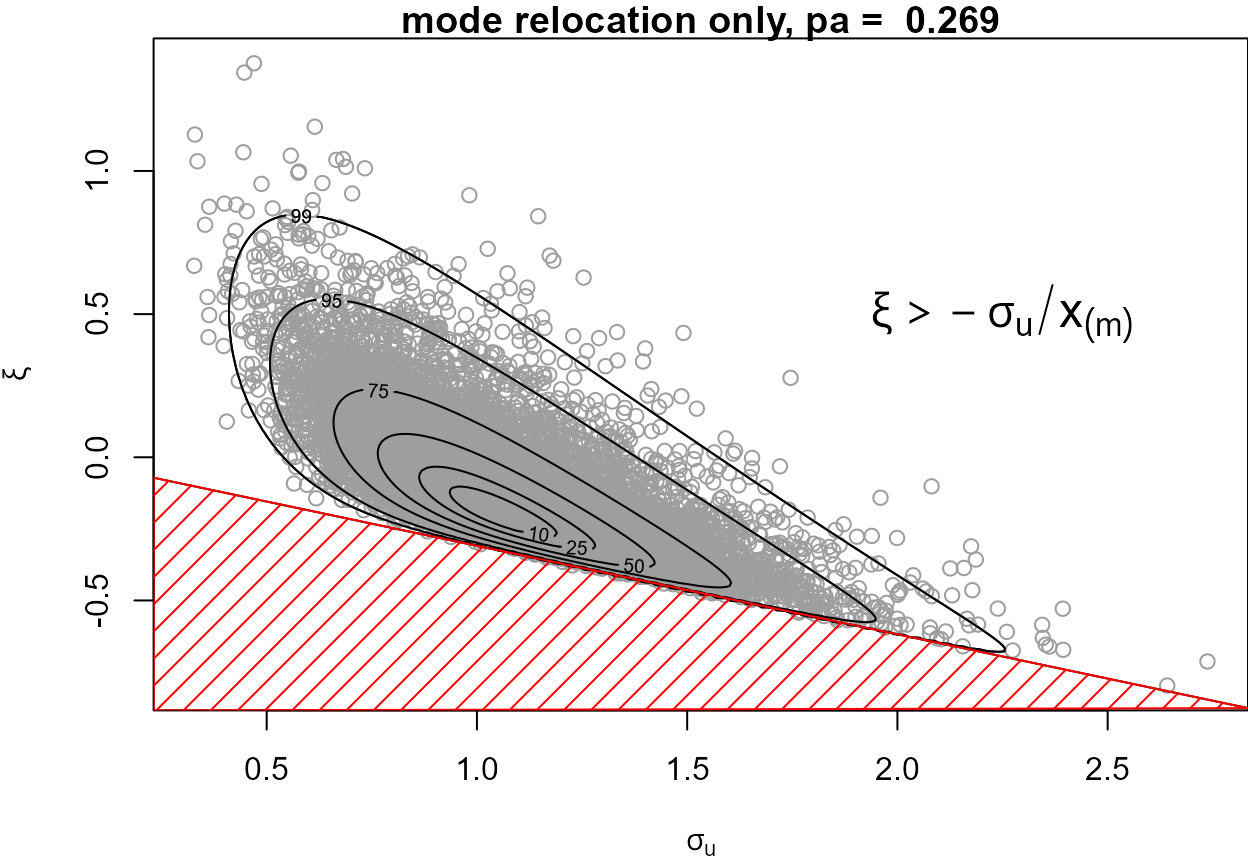
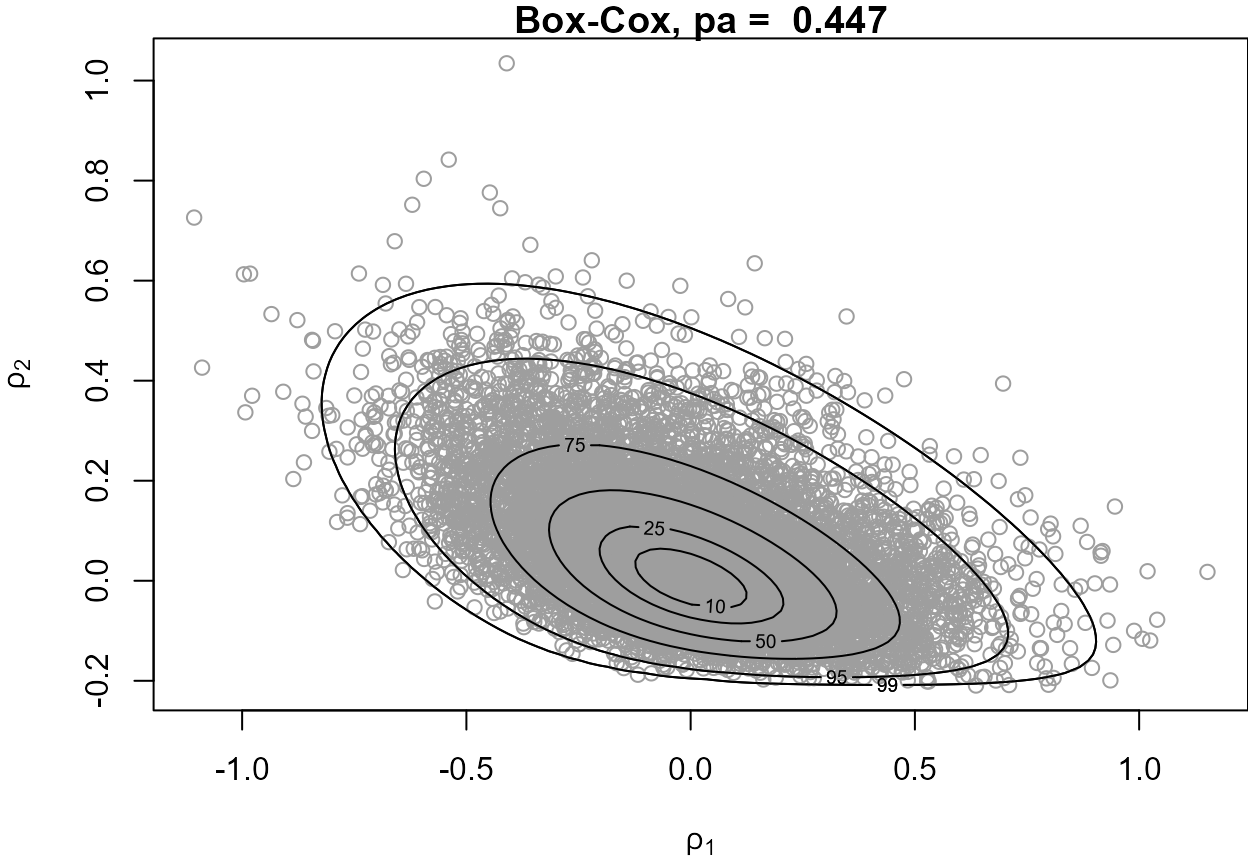
\[ p_a(d, r) = \frac{\int f(x) {\rm ~d}x}{(r d + 1) \, a(r) \displaystyle\prod_{i=1}^d \left[b_i^+(r) -b_i^-(r) \right]} \]

Relocate the mode to zero (hard-coded into rust)
Choice of \(r\) (\(r = 1/2\) optimal for zero-mean normal)
Rotation (\(d > 1\)): the weaker the association the better
Transformation: symmetric better than asymmetric

(EV posteriors can exhibit strong dependence and asymmetry)

rust R package
Introduction to rust vignette

Acceptance region for N(10, 1)

R exercises 1

1D normal
1D log-normal
2D normal
1D gamma

For fun!

Can you find simple (1D) examples that throw

a warning?
an error?

Use ?Distributions for possibilities

Summary of ROU and rust

Can be useful for
- suitable low-dimensional distributions
- for which a bespoke method does not exist
Box-Cox transformation requires positive variable(s)
- to do: generalise to Yeo-Johnson transformation
Cannot be used in all cases
- unbounded densities: perhaps OK after transformation
- heavy tails: choose \(r\) appropriately and/or transform
- multi-modal: OK in theory, but need to find global optima

See When can rust be used?

Bayesian EV analyses

Prior \(\pi(\theta)\) for model parameter vector \(\theta\)
Likelihood \(L(\theta \mid \mbox{data})\)
Posterior \(\pi(\theta \mid \mbox{data})\) via Bayes’ theorem \[ \pi(\theta \mid \mbox{data}) = \frac{L(\theta \mid \mbox{data}) \pi(\theta)}{P(\mbox{data})} = \frac{L(\theta \mid \mbox{data}) \pi(\theta)}{\int L(\theta \mid \mbox{data}) \pi(\theta) \,\mbox{d}\theta} \]
Simulate a large sample from \(\pi(\theta \mid \mbox{data})\), often using MCMC

In revdbayes

4 standard univariate models: GEV, OS, GP, PP
Simplest, i.i.d. case

GP model for threshold excesses 1

Negative association + asymmetry \(\phantom{\xi + \sigma / x_{(m)}}\)

GP model for threshold excesses 2

Rotation about the MAP estimate based on the Hessian at the MAP \(\phantom{\xi + \sigma / x_{(m)}}\)

GP model for threshold excesses 3

Box-Cox transformations of \(\phi_1 = \sigma_u > 0\) and \(\phi_2 = \xi + \sigma / x_{(m)} > 0\)

GP model for threshold excesses 4

Box-Cox first then rotate \(\phantom{\xi + \sigma / x_{(m)}}\)

Other models in revdbayes

GEV for block (annual?) maxima
Order statistics (OS): largest \(k\) observations per block
Non-homogeneous point process (PP) for threshold exceedances
- approximates binomial for threshold exceedance and GP for excesses
- GEV parameterisation: \((\mu, \sigma, \xi)\)
- choice of block length affects posterior sampling efficiency

R exercises 2

GP and binomial-GP
- compare ROU posterior sampling approaches
- posterior predictive model checking
- predictive inference
PP: sampling efficiently from the posterior
GEV: compare revdbayes and evdbayes

Options to experiment

changing threshold
playing with function arguments

Reflections