Predictive inference for the largest value observed in $N$ years.

predict method for class "evpost". Performs predictive inference about the largest value to be observed over a future time period of $N$ years. Predictive inferences accounts for uncertainty in model parameters and for uncertainty owing to the variability of future observations.

Usage

# S3 method for class 'evpost'
predict(
  object,
  type = c("i", "p", "d", "q", "r"),
  x = NULL,
  x_num = 100,
  n_years = 100,
  npy = NULL,
  level = 95,
  hpd = FALSE,
  lower_tail = TRUE,
  log = FALSE,
  big_q = 1000,
  ...
)

Arguments

object

An object of class "evpost", a result of a call to rpost or rpost_rcpp with model = "gev", model = "os", model = "pp" or model == "bingp". Calling these functions after a call to rpost or rpost_rcpp with model == "gp" will produce an error, because inferences about the probability of threshold exceedance are required, in addition to the distribution of threshold excesses. The model is stored in object$model.

object may also be an object created within the function predict.blite in the lite package. In this case object$sim_vals has a column named "theta" containing a posterior sample of values of the extremal index.

type

A character vector. Indicates which type of inference is required:

"i" for predictive intervals,
"p" for the predictive distribution function,
"d" for the predictive density function,
"q" for the predictive quantile function,
"r" for random generation from the predictive distribution.

x

A numeric vector or a matrix with n_years columns. The meaning of x depends on type.

type = "p" or type = "d": x contains quantiles at which to evaluate the distribution or density function.

If object$model == "bingp" then no element of x can be less than the threshold object$thresh.

If x is not supplied then n_year-specific defaults are set: vectors of length x_num from the 0.1% quantile to the 99% quantile, subject all values being greater than the threshold.
type = "q": x contains probabilities in (0,1) at which to evaluate the quantile function. Any values outside (0, 1) will be removed without warning.

If object$model == "bingp" then no element of p can correspond to a predictive quantile that is below the threshold, object$thresh. That is, no element of p can be less than the value of predict.evpost(object, type = "q", x = object$thresh).

If x is not supplied then a default value of c(0.025, 0.25, 0.5, 0.75, 0.975) is used.
type = "i" or type = "r": x is not relevant.

x_num

A numeric scalar. If type = "p" or type = "d" and x is not supplied then x_num gives the number of values in x for each value in n_years.

n_years

A numeric vector. Values of $N$.

npy

A numeric scalar. The mean number of observations per year of data, after excluding any missing values, i.e. the number of non-missing observations divided by total number of years' worth of non-missing data.

If rpost or rpost_rcpp was called with model == "bingp" then npy must either have been supplied in that call or be supplied here.

Otherwise, a default value will be assumed if npy is not supplied, based on the value of model in the call to rpost or rpost_rcpp:

model = "gev": npy = 1, i.e. the data were annual maxima so the block size is one year.
model = "os": npy = 1, i.e. the data were annual order statistics so the block size is one year.
model = "pp": npy = length(x$data) / object$noy, i.e. the value of noy used in the call to rpost or rpost_rcpp is equated to a block size of one year.

If npy is supplied twice then the value supplied here will be used and a warning given.

level

A numeric vector of values in (0, 100). Only relevant when type = "i". Levels of predictive intervals for the largest value observed in $N$ years, i.e. level% predictive intervals are returned.

hpd

A logical scalar. Only relevant when type = "i".

If hpd = FALSE then the interval is equi-tailed, with its limits produced by
predict.evpost(object, type ="q", x = p), where p = c((1-level/100)/2, (1+level/100)/2).

If hpd = TRUE then, in addition to the equi-tailed interval, the shortest possible level% interval is calculated. If the predictive distribution is unimodal then this is a highest predictive density (HPD) interval.

lower_tail

A logical scalar. Only relevant when type = "p" or type = "q". If TRUE (default), (output or input) probabilities are $P[X \leq x]$, otherwise, $P[X > x]$.

log

A logical scalar. Only relevant when type = "d". If TRUE the log-density is returned.

big_q

A numeric scalar. Only relevant when type = "q". An initial upper bound for the desired quantiles to be passed to uniroot (its argument upper) in the search for the predictive quantiles. If this is not sufficiently large then it is increased until it does provide an upper bound.

...

Additional optional arguments. At present no optional arguments are used.

Value

An object of class "evpred", a list containing a subset of the following components:

type

The argument type supplied to predict.evpost. Which of the following components are present depends type.

x

A matrix containing the argument x supplied to predict.evpost, or set within predict.evpost if x was not supplied, replicated to have n_years columns if necessary. Only present if type is "p", "d" or "q".

y

The content of y depends on type:

type = "p", "d", "q": A matrix with the same dimensions as x. Contains distribution function values (type = "p"), predictive density (type = "d") or quantiles (type = "q").
type = "r": A numeric matrix with length(n_years) columns and number of rows equal to the size of the posterior sample.
type = "i": y is not present.

long

A length(n_years)*length(level) by 4 numeric matrix containing the equi-tailed limits with columns: lower limit, upper limit, n_years, level. Only present if type = "i". If an interval extends below the threshold then NA is returned.

short

A matrix with the same structure as long containing the HPD limits. Only present if type = "i". Columns 1 and 2 contain NAs if hpd = FALSE or if the corresponding equi-tailed interval extends below the threshold.

The arguments n_years, level, hpd, lower_tail, log supplied to predict.evpost are also included, as is the argument npy supplied to, or set within, predict.evpost and the arguments data and model from the original call to rpost or rpost_rcpp.

Details

Inferences about future extreme observations are integrated over the posterior distribution of the model parameters, thereby accounting for uncertainty in model parameters and uncertainty owing to the variability of future observations. In practice the integrals involved are estimated using an empirical mean over the posterior sample. See, for example, Coles (2001), Stephenson (2016) or Northrop et al. (2017) for details. See also the vignette Posterior Predictive Extreme Value Inference

GEV / OS / PP. If model = "gev", model = "os" or model = "pp" in the call to rpost or rpost_rcpp we first calculate the number of blocks $b$ in n_years years. To calculate the density function or distribution function of the maximum over n_years we call dgev or pgev with m = $b$.

type = "p". We calculate using pgev the GEV distribution function at q for each of the posterior samples of the location, scale and shape parameters. Then we take the mean of these values.
type = "d". We calculate using dgev the GEV density function at x for each of the posterior samples of the location, scale and shape parameters. Then we take the mean of these values.
type = "q". We solve numerically predict.evpost(object, type = "p", x = q) = p[i] numerically for q for each element p[i] of p.
type = "i". If hpd = FALSE then the interval is equi-tailed, equal to predict.evpost() object, type ="q", x = p), where p = c((1-level/100)/2, (1+level/100)/2). If hpd = TRUE then, in addition, we perform a numerical minimisation of the length of level% intervals, after approximating the predictive quantile function using monotonic cubic splines, to reduce computing time.
type = "r". For each simulated value of the GEV parameters at the n_years level of aggregation we simulate one value from this GEV distribution using rgev. Thus, each sample from the predictive distribution is of a size equal to the size of the posterior sample.

Binomial-GP. If model = "bingp" in the call to rpost or rpost_rcpp then we calculate the mean number of observations in n_years years, i.e. npy * n_years.

Following Northrop et al. (2017), let $M_N$ be the largest value observed in $N$ years, $m$ = npy * n_years and $u$ the threshold object$thresh used in the call to rpost or rpost_rcpp. For fixed values of $\theta = (p, \sigma, \xi)$ the distribution function of $M_N$ is given by $F(z, \theta)^m$, for $z \geq u$, where $$F(z, \theta) = 1 - p [1 + \xi (x - u) / \sigma] ^ {-1/\xi}.$$ The distribution function of $M_N$ cannot be evaluated for $z < u$ because no model has been supposed for observations below the threshold.

type = "p". We calculate $F(z, \theta)^m$ at q for each of the posterior samples $\theta$. Then we take the mean of these values.
type = "d". We calculate the density of of $M_n$, i.e. the derivative of $F(z, \theta)^m$ with respect to $z$ at x for each of the posterior samples $\theta$. Then we take the mean of these values.
type = "q" and type = "i". We perform calculations that are analogous to the GEV case above. If n_years is very small and/or level is very close to 100 then a predictive interval may extend below the threshold. In such cases NAs are returned (see Value below).
type = "r". For each simulated value of the bin-GP parameter we simulate from the distribution of $M_N$ using the inversion method applied to the distribution function of $M_N$ given above. Occasionally a value below the threshold would need to be simulated. If these instances a missing value code NA is returned. Thus, each sample from the predictive distribution is of a size equal to the size of the posterior sample, perhaps with a small number os NAs.

References

Coles, S. G. (2001) An Introduction to Statistical Modeling of Extreme Values, Springer-Verlag, London. Chapter 9: doi:10.1007/978-1-4471-3675-0_9

Northrop, P. J., Attalides, N. and Jonathan, P. (2017) Cross-validatory extreme value threshold selection and uncertainty with application to ocean storm severity. Journal of the Royal Statistical Society Series C: Applied Statistics, 66(1), 93-120. doi:10.1111/rssc.12159

Stephenson, A. (2016). Bayesian Inference for Extreme Value Modelling. In Extreme Value Modeling and Risk Analysis: Methods and Applications, edited by D. K. Dey and J. Yan, 257-80. London: Chapman and Hall. doi:10.1201/b19721

Examples

### GEV
data(portpirie)
mat <- diag(c(10000, 10000, 100))
pn <- set_prior(prior = "norm", model = "gev", mean = c(0,0,0), cov = mat)
gevp  <- rpost_rcpp(n = 1000, model = "gev", prior = pn, data = portpirie)

# Interval estimation
predict(gevp)$long
#>         lower    upper n_years level
#> [1,] 4.451427 6.059904     100    95
predict(gevp, hpd = TRUE)$short
#>       lower    upper n_years level
#> [1,] 4.3686 5.723977     100    95
# Density function
x <- 4:7
predict(gevp, type = "d", x = x)$y
#>              [,1]
#> [1,] 9.987568e-15
#> [2,] 7.838839e-01
#> [3,] 4.924776e-02
#> [4,] 7.666987e-03
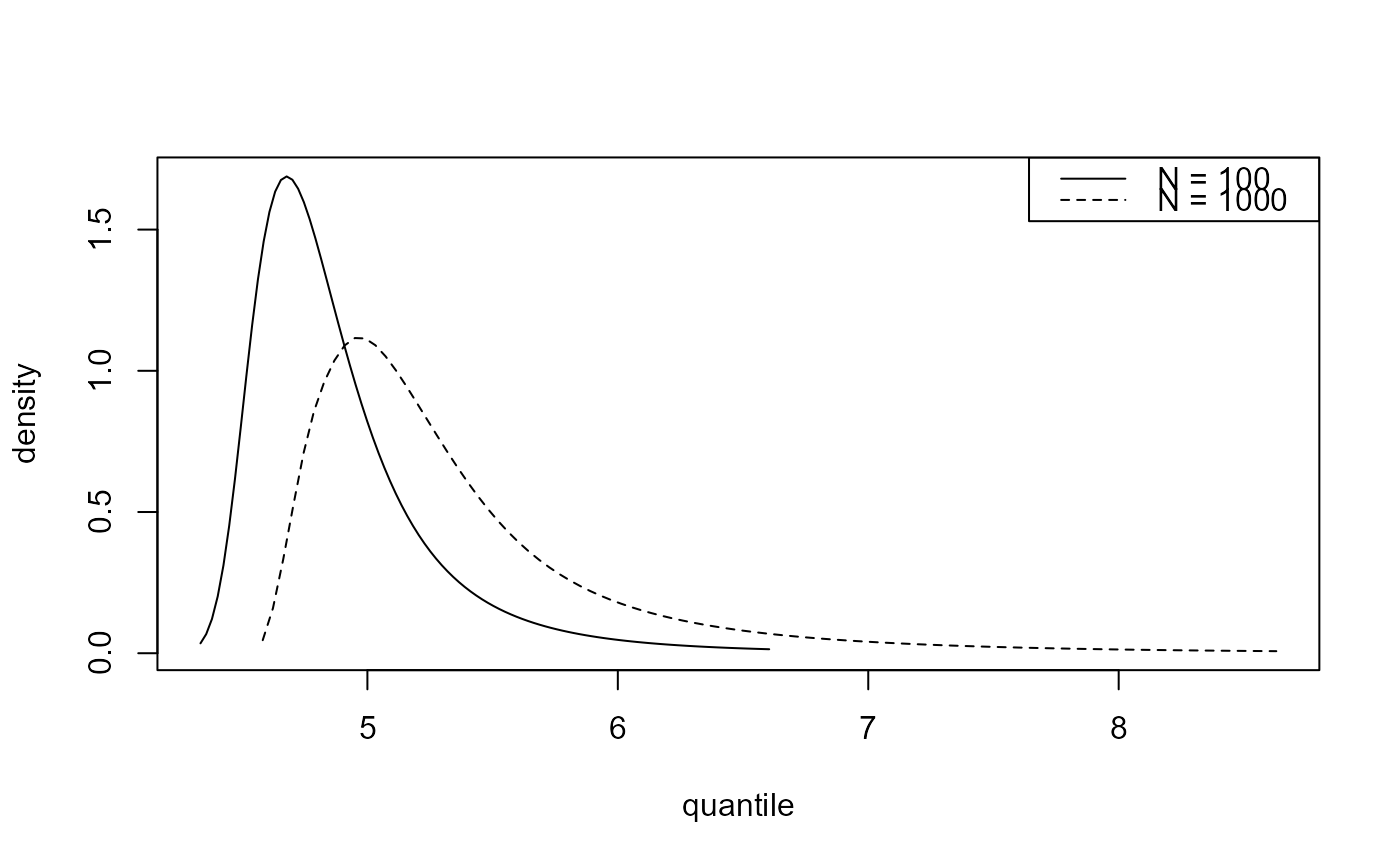
plot(predict(gevp, type = "d", n_years = c(100, 1000)))

# Distribution function
predict(gevp, type = "p", x = x)$y
#>              [,1]
#> [1,] 5.424865e-17
#> [2,] 7.239008e-01
#> [3,] 9.722400e-01
#> [4,] 9.933130e-01
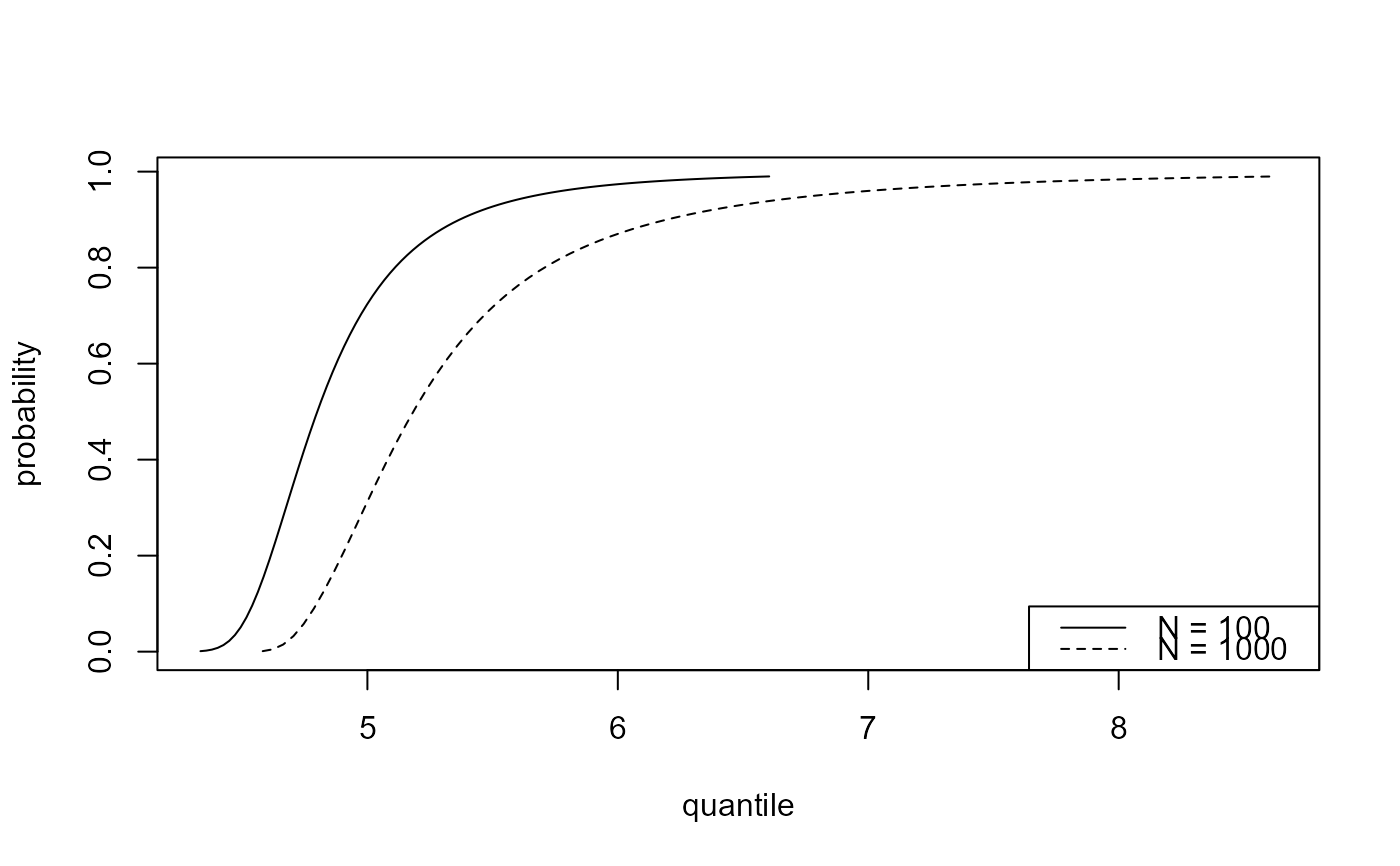
plot(predict(gevp, type = "p", n_years = c(100, 1000)))

# Quantiles
predict(gevp, type = "q", n_years = c(100, 1000))$y
#>          [,1]     [,2]
#> [1,] 4.451427 4.682122
#> [2,] 4.637908 4.914086
#> [3,] 4.792871 5.166369
#> [4,] 5.035141 5.595984
#> [5,] 6.059904 7.492340
# Random generation
plot(predict(gevp, type = "r"))


### Binomial-GP
u <- quantile(gom, probs = 0.65)
fp <- set_prior(prior = "flat", model = "gp", min_xi = -1)
bp <- set_bin_prior(prior = "jeffreys")
npy_gom <- length(gom)/105
bgpg <- rpost_rcpp(n = 1000, model = "bingp", prior = fp, thresh = u,
                   data = gom, bin_prior = bp)

# Setting npy in call to predict.evpost()
predict(bgpg, npy = npy_gom)$long
#>         lower    upper n_years level
#> [1,] 10.44688 43.13816     100    95

# Setting npy in call to rpost() or rpost_rcpp()
bgpg <- rpost_rcpp(n = 1000, model = "bingp", prior = fp, thresh = u,
                   data = gom, bin_prior = bp, npy = npy_gom)

# Interval estimation
predict(bgpg)$long
#>         lower    upper n_years level
#> [1,] 10.36896 40.13727     100    95
predict(bgpg, hpd = TRUE)$short
#>         lower    upper n_years level
#> [1,] 9.022362 32.73721     100    95
# Density function
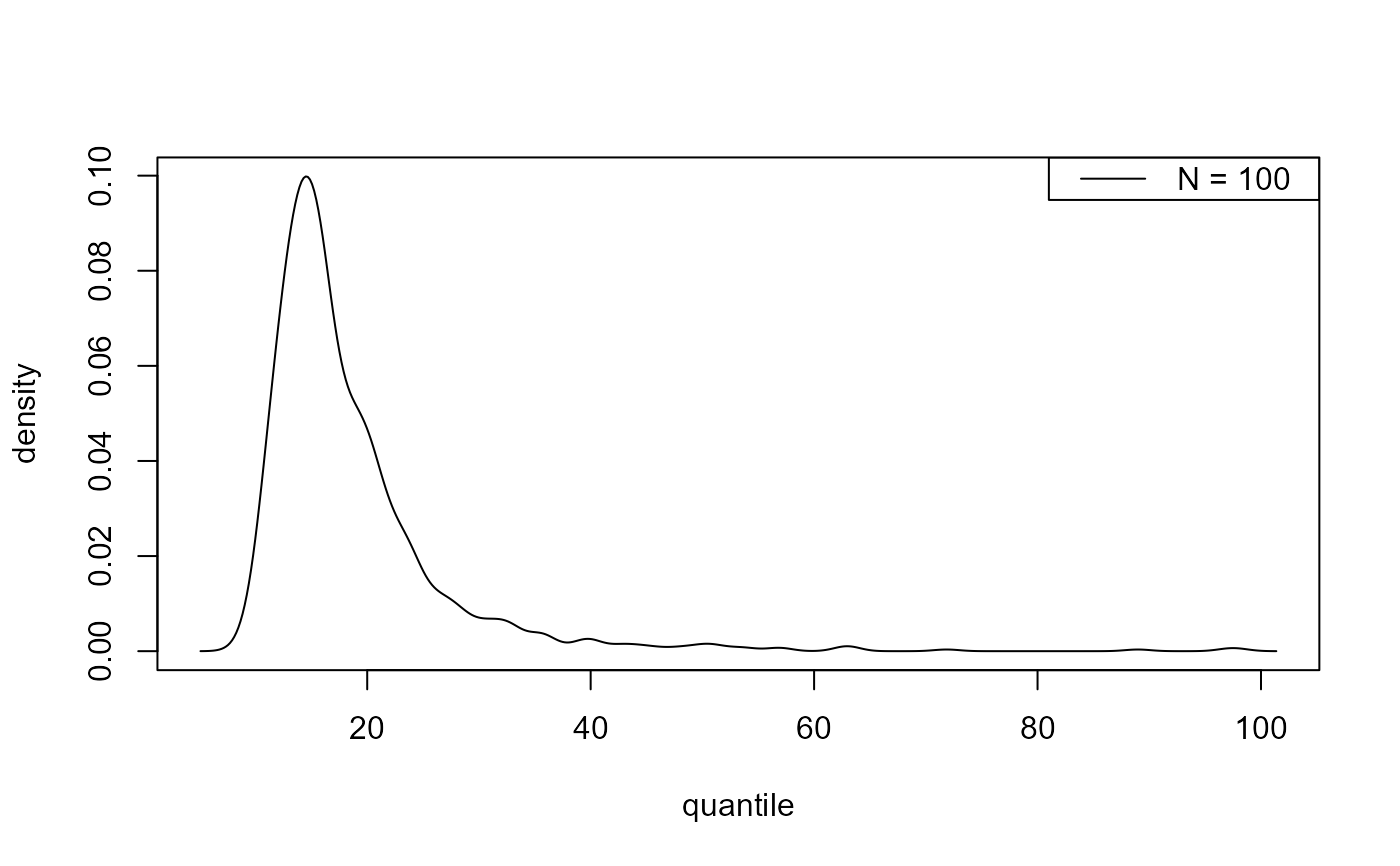
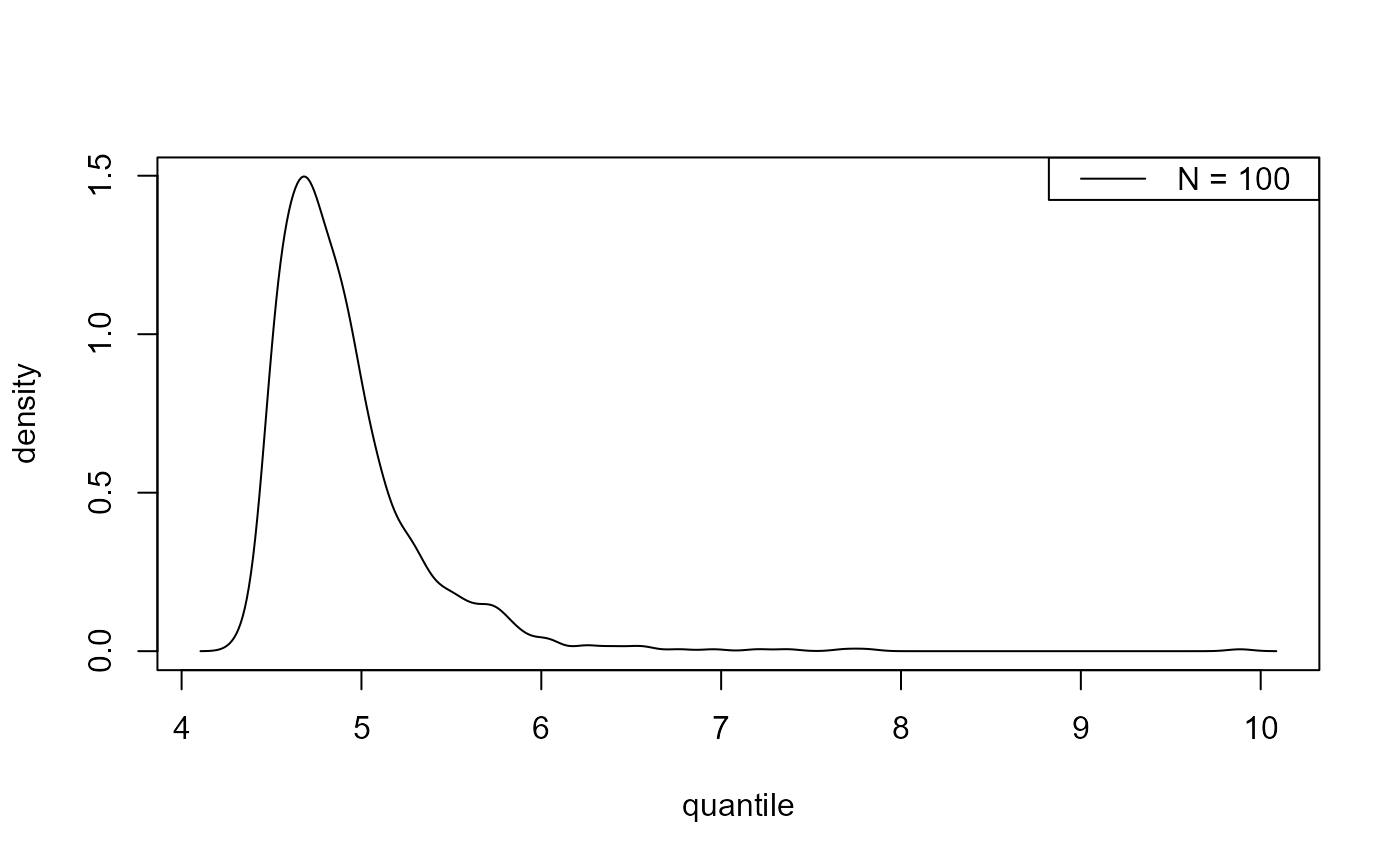
plot(predict(bgpg, type = "d", n_years = c(100, 1000)))

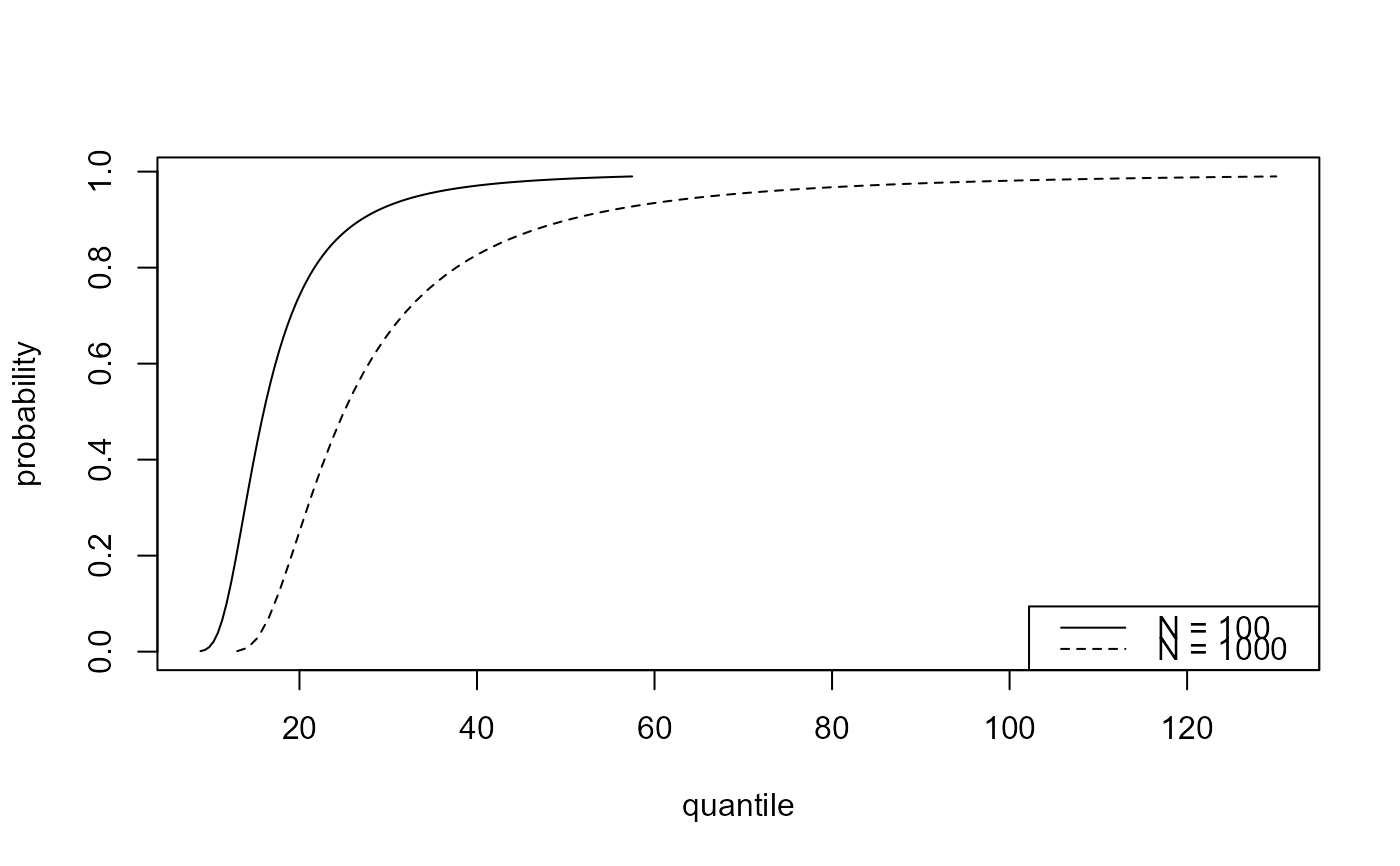
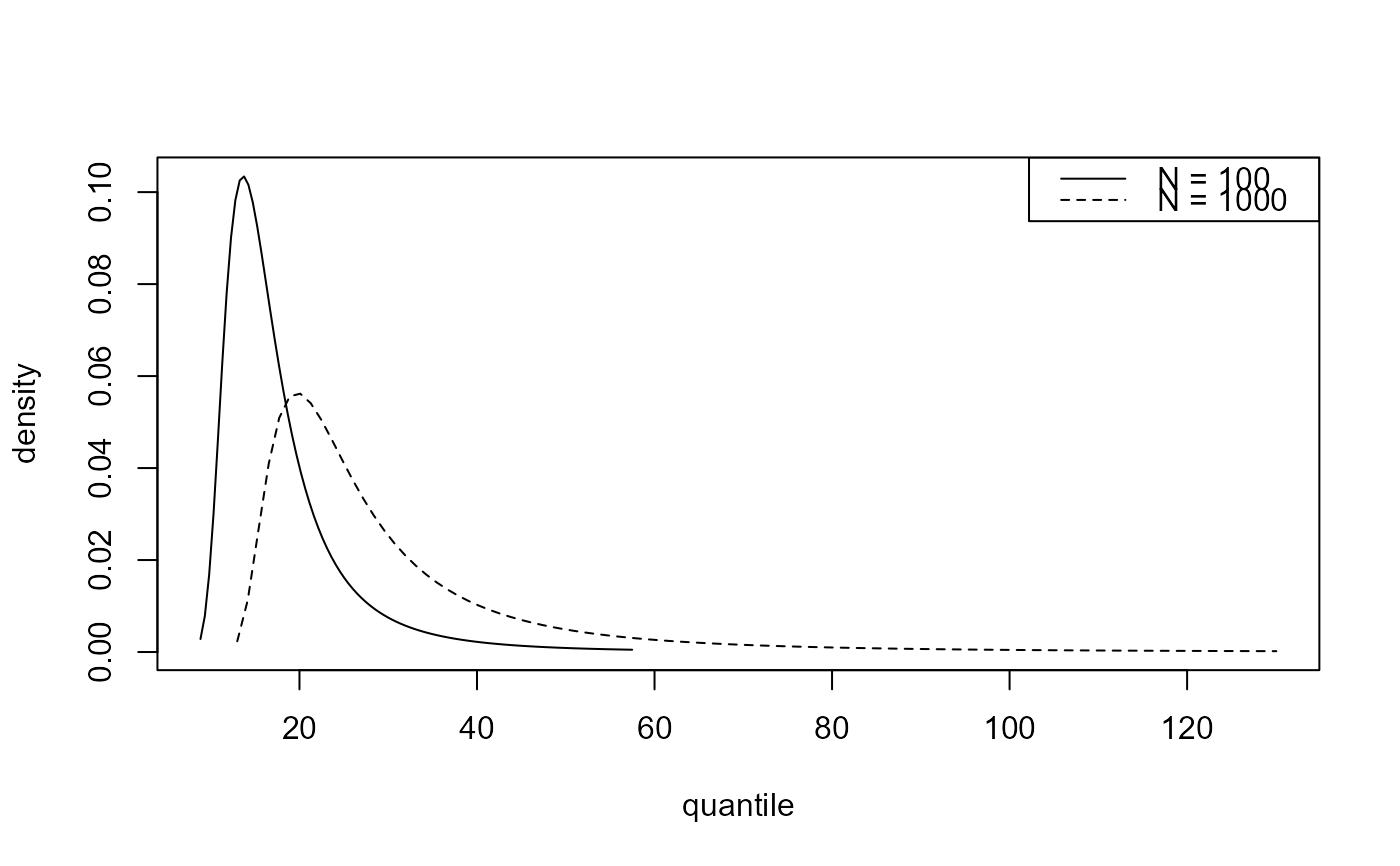# Distribution function
plot(predict(bgpg, type = "p", n_years = c(100, 1000)))

# Quantiles
predict(bgpg, type = "q", n_years = c(100, 1000))$y
#>          [,1]     [,2]
#> [1,] 10.36896 14.89904
#> [2,] 13.23340 19.63675
#> [3,] 15.75439 24.55749
#> [4,] 19.83773 33.29166
#> [5,] 40.13727 81.41772
# Random generation
plot(predict(bgpg, type = "r"))

Predictive inference for the largest value observed in \(N\) years.