Chapter 6: binomial, geometric and Poisson distributions
Paul Northrop
Source:vignettes/stat0002-ch6a-discrete-random-variables-vignette.Rmd
stat0002-ch6a-discrete-random-variables-vignette.RmdThe purposes of this vignette are to direct you to R functions relating to the discrete probability distributions considered in Chapter 6 of the STAT0002 notes and to provide code to do some of the things that appear in the lecture slides. First, we do this using the standard R functions (in the stats package). Then we repeat some of the calculations using the distributions3 package (Hayes and Moller-Trane 2019), which provides a neat way to work with random variables in R.
We illustrate these functions using the Australian birth times data,
which are available in the data frame aussie_births.
> library(stat0002)
> head(aussie_births)
time sex weight
1 5 girl 3837
2 64 girl 3334
3 78 boy 3554
4 115 boy 3838
5 177 boy 3625
6 245 girl 2208The stats package contains functions to evaluate the
probability mass function (p.m.f.), cumulative distribution function
(c.d.f.) and quantile function (which could also be called the inverse
c.d.f.) of many discrete probability distributions, including the
binomial, geometric and Poisson. It also contains functions to simulate
random variates from these distributions. For a general description of
these functions use ?Distributions. These functions are
named in the following way, where xxx is the name (perhaps
abbreviated) of the distribution in question: dxxx (p.m.f),
pxxx (c.d.f), qxxx (quantile function) and
rxxx (random variate generation).
The binomial distribution
Following the STAT0002 notes, let us suppose that (before we observe the data) the number \(Y\) of boy babies is a random variable with a binomial(44, \(p\)) distribution, where \(p\) is the probability that a randomly chosen birth produces a boy. We use the data to estimate \(p\).
> nboys <- sum(aussie_births[, "sex"] == "boy")
> ngirls <- sum(aussie_births[, "sex"] == "girl")
> phat <- nboys / (nboys + ngirls)
> phat
[1] 0.5909091The function dbinom evaluates the p.m.f. of a binomial
distribution. See ?Binomial for information about this
function and pbinom, qbinom and
rbinom. The following code produces a plot that is similar
to the ones we looked at in a lecture. You could vary p,
perhaps setting it to be equal to phat, and see the effect
on the p.m.f. of the binomial distribution.
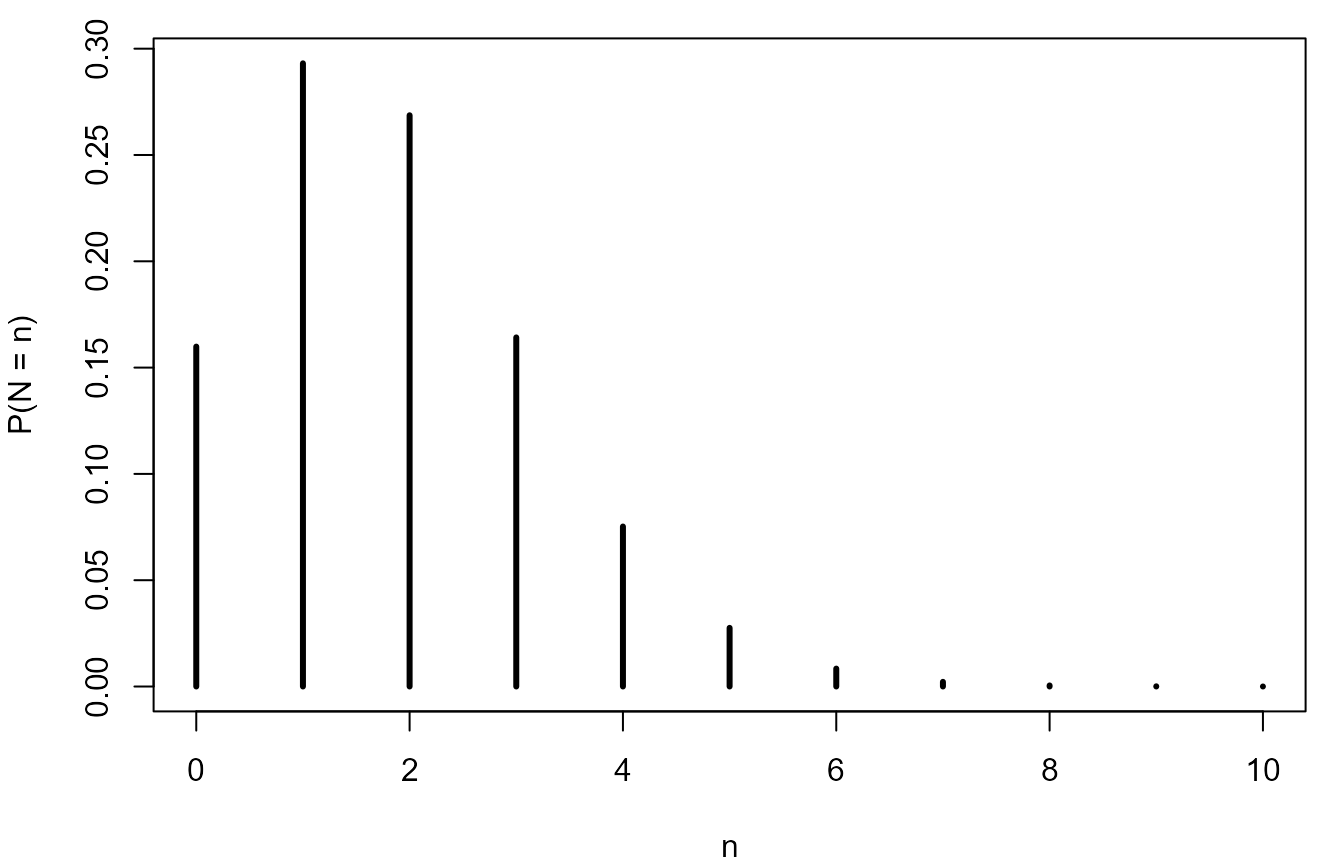
> # Plot the binomial(44, 1/2) p.m.f.
> n <- nboys + ngirls
> p <- 1 / 2
> y <- 0:n
> # Note that dbinom calculates the probabilities all values in the vector y
> plot(y, dbinom(y, n, p), type = "h", lwd = 3, ylab = "P(Y = y)", xlab = "y")
For the purposes of illustrating how the functions
pbinom, qbinom and rbinom work,
let us suppose that \(p = 1/2\). We
used the values of the following probabilities during a lecture, when we
considered how surprised we might to observe a number of boys 4 or more
from the expected value of 22 under the hypothesis that \(p = 1/2\).
> # Calculate P(Y >= 26) = P(Y > 25) and P(Y <= 18)
> pbinom(25, size = n, prob = 1 / 2, lower.tail = FALSE)
[1] 0.1456076
> pbinom(18, n, 1 / 2)
[1] 0.1456076Suppose that we want to find the median of \(Y\). We can use qbinom:
> qbinom(1 / 2, n, 1 / 2)
[1] 22
> # A check (look at the definition of the median in the notes)
> pbinom(21:23, n, 1 / 2)
[1] 0.4401979 0.5598021 0.6742061The following code simulates 100 values from a Binomial(44, 1/2) distribution.
> ysim <- rbinom(100, 44, 1 / 2)
> ysim
[1] 22 26 22 18 22 30 24 24 20 21 18 21 22 24 19 20 26 22 24 17 23 20 16 24 26
[26] 24 17 24 25 18 20 18 24 24 24 27 19 22 18 21 20 25 26 22 21 25 22 25 23 22
[51] 21 22 26 23 21 28 20 23 22 23 26 23 22 22 19 23 23 19 27 23 27 21 24 21 22
[76] 25 18 22 23 23 20 24 24 28 21 21 21 25 25 23 21 24 23 30 28 19 26 28 20 21
> summary(ysim)
Min. 1st Qu. Median Mean 3rd Qu. Max.
16.00 21.00 22.50 22.61 24.00 30.00 The distributions3 package
In September 2019 the distributions3 package (Hayes and Moller-Trane 2019) was released. A
neat feature of this package is that it enables us to create an R object
that corresponds to a particular random variable. Then we are able
easily to use some simple R functions to perform calculations with this
random variable. The way that this works is perhaps more intuitive than
the way in which we use functions like dbinom() above.
> library(distributions3)
Attaching package: 'distributions3'
The following object is masked from 'package:stats':
Gamma
The following object is masked from 'package:grDevices':
pdf
> # (The warnings tell us that the distributions3 package has functions with the
> # same names as functions from other packages and has `masked' them, that is,
> # R will use these functions from distributions3, not the other functions.)
> #
> # Create an R object that is, effectively, a binomial(n, 1/2) random variable
> Y <- Binomial(n, 1 / 2)
> Y
[1] "Binomial(size = 44, p = 0.5)"We reproduce the plot and repeat the calculation of the probabilities.
> # Reproduce the plot.
> plot(0:n, pmf(Y, 0:n), type = "h", lwd = 3, ylab = "P(X = x)", xlab = "x")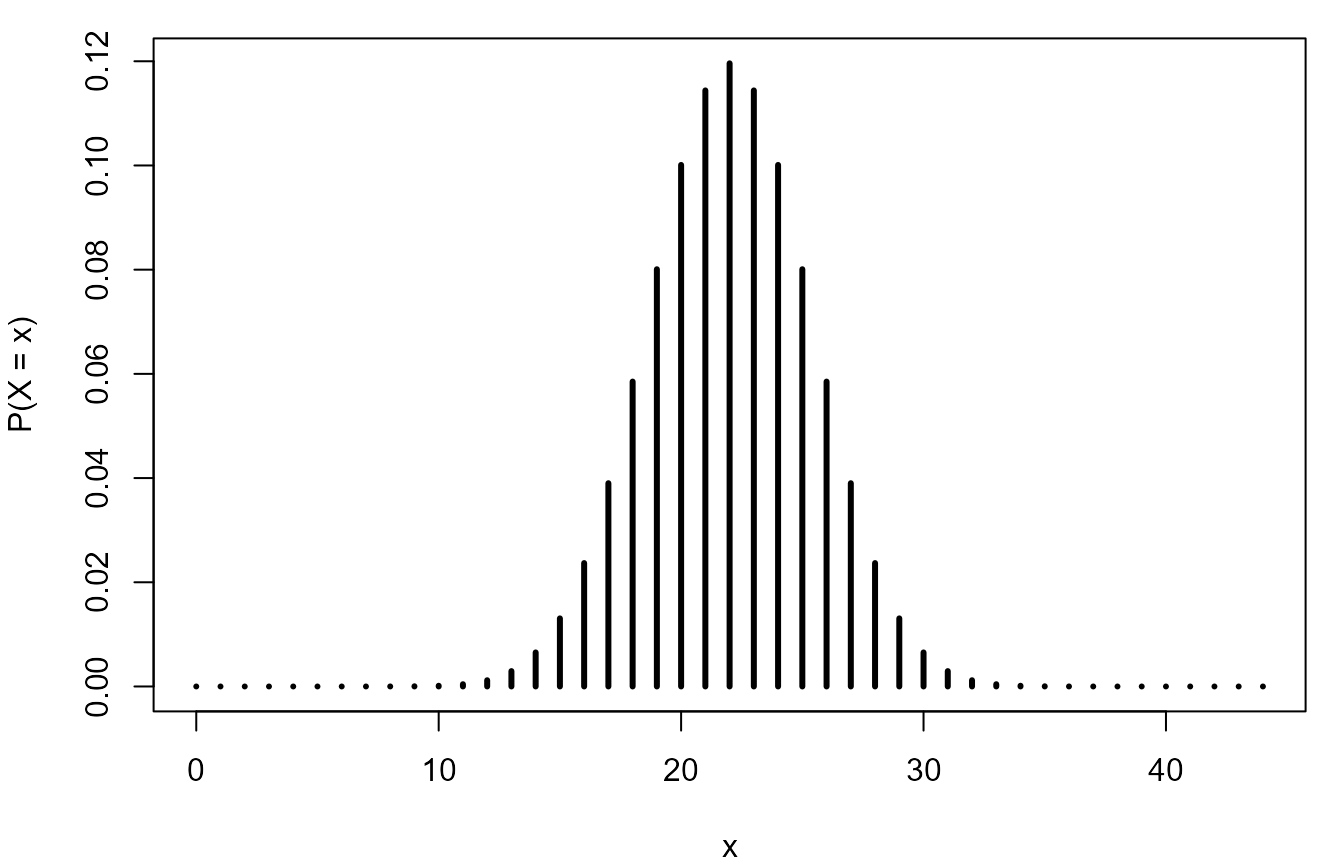
Now we use the distributions package to performs some of the calculations that were involved in producing the lecture slides associated with the geometric and Poisson distributions.
The geometric distribution
We recreate the table in the lecture slides, of the observed frequencies and proportions and the corresponding estimated expected values under a geometric distribution fitted to the data.
R’s dgeom function, and the function
Geometric in the distributions package,
are is based on the number of failures before the first success, not the
number of trials. Therefore, we subtract 1 below when we call the
function dgeom.
> # Observed, adding a zero for greater than or equal to 6
> geom <- diff(c(0, which(aussie_births$sex == "boy")))
> max_w <- max(geom)
> geom <- c(1:(max_w + 1), geom)
> obs_freq <- table(geom) - 1
> obs_prop <- obs_freq / sum(obs_freq)
> round(obs_prop, 3)
geom
1 2 3 4 5 6
0.692 0.115 0.154 0.000 0.038 0.000
>
> # Estimated expected, using dgeom
> est_prob <- dgeom((1:max_w) - 1, prob = phat)
> est_prob <- c(est_prob, 1 - sum(est_prob))
> exp_freq <- nboys * est_prob
>
> # The table
> round(cbind(w = 1:(max_w + 1), obs_freq, exp_freq, obs_prop, est_prob), 3)
w obs_freq exp_freq obs_prop est_prob
1 1 18 15.364 0.692 0.591
2 2 3 6.285 0.115 0.242
3 3 4 2.571 0.154 0.099
4 4 0 1.052 0.000 0.040
5 5 1 0.430 0.038 0.017
6 6 0 0.298 0.000 0.011Alternatively, We could also use the distributions3 package to calculate the probabilities that we require.
The Poisson distribution
Here we use the distributions package to produce a plot of the p.m.f. of the Poisson(\(\hat{\lambda}\)) distribution, where \(\hat{\lambda}\) is equal to the sample mean of the numbers of babies born in each of the 24 hourly periods. We also calculate the probabilities involved in the table of observed and estimated expected frequencies given in the lecture.