Chapter 10: Correlation

Paul Northrop

This vignette provides some R code that is related to some of the content of Chapter 10 of the STAT0002 notes correlation.

> library(stat0002)

Example data

We use the exchange rate data described at the start of Section 10.1 of the notes. These data are available in the data frame exchange. We look at the first 6 rows of the data and the last 6 rows and produce plots like Figures 10.1 and 10.2 of the notes.

> head(exchange)
           USD.GBP CAD.GBP
1997/01/02  1.6865  2.3167
1997/01/03  1.6905  2.3224
1997/01/06  1.6855  2.3056
1997/01/07  1.6951  2.2999
1997/01/08  1.6884  2.2850
1997/01/09  1.6947  2.2906
> tail(exchange)
           USD.GBP CAD.GBP
2000/11/14  1.4309  2.2102
2000/11/15  1.4265  2.2121
2000/11/16  1.4229  2.2088
2000/11/17  1.4233  2.2194
2000/11/20  1.4223  2.2172
2000/11/21  1.4169  2.2029
> # Figure 10.1
> plot(exchange, pch = 16, xlab = "Pounds sterling vs. US dollars",
+      ylab = "Pounds sterling vs. Canadian dollars", bty = "l", 
+      main = "Raw data")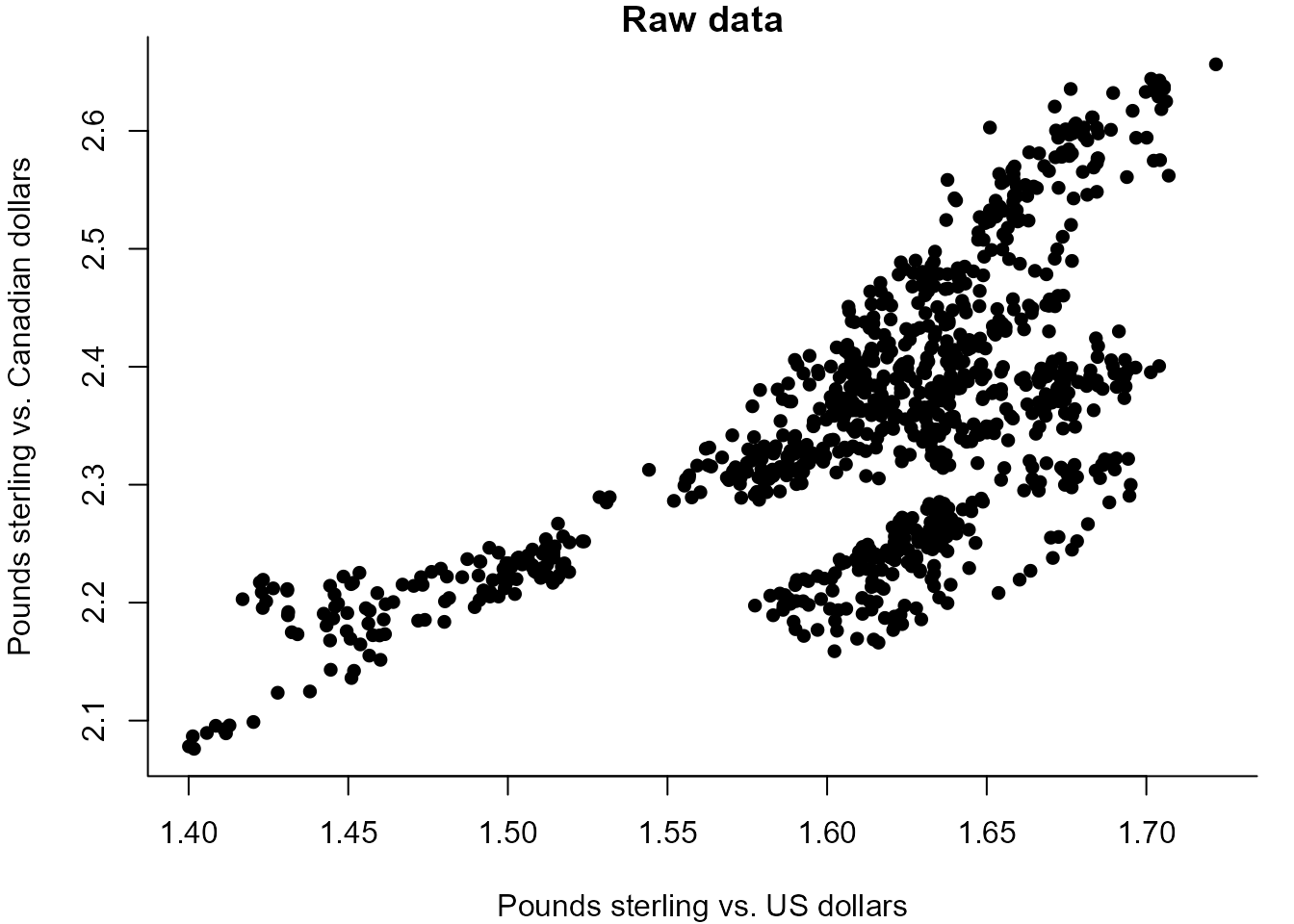

> # Calculate the log-returns
> USDlogr <- diff(log(exchange$USD.GBP))
> CADlogr <- diff(log(exchange$CAD.GBP))
> # Figure 10.2
> plot(USDlogr, CADlogr, pch = 16, xlab = "Pounds sterling vs. US dollars",
+      ylab = "Pounds sterling vs. Canadian dollars", bty = "l", 
+      main = "Log-returns" )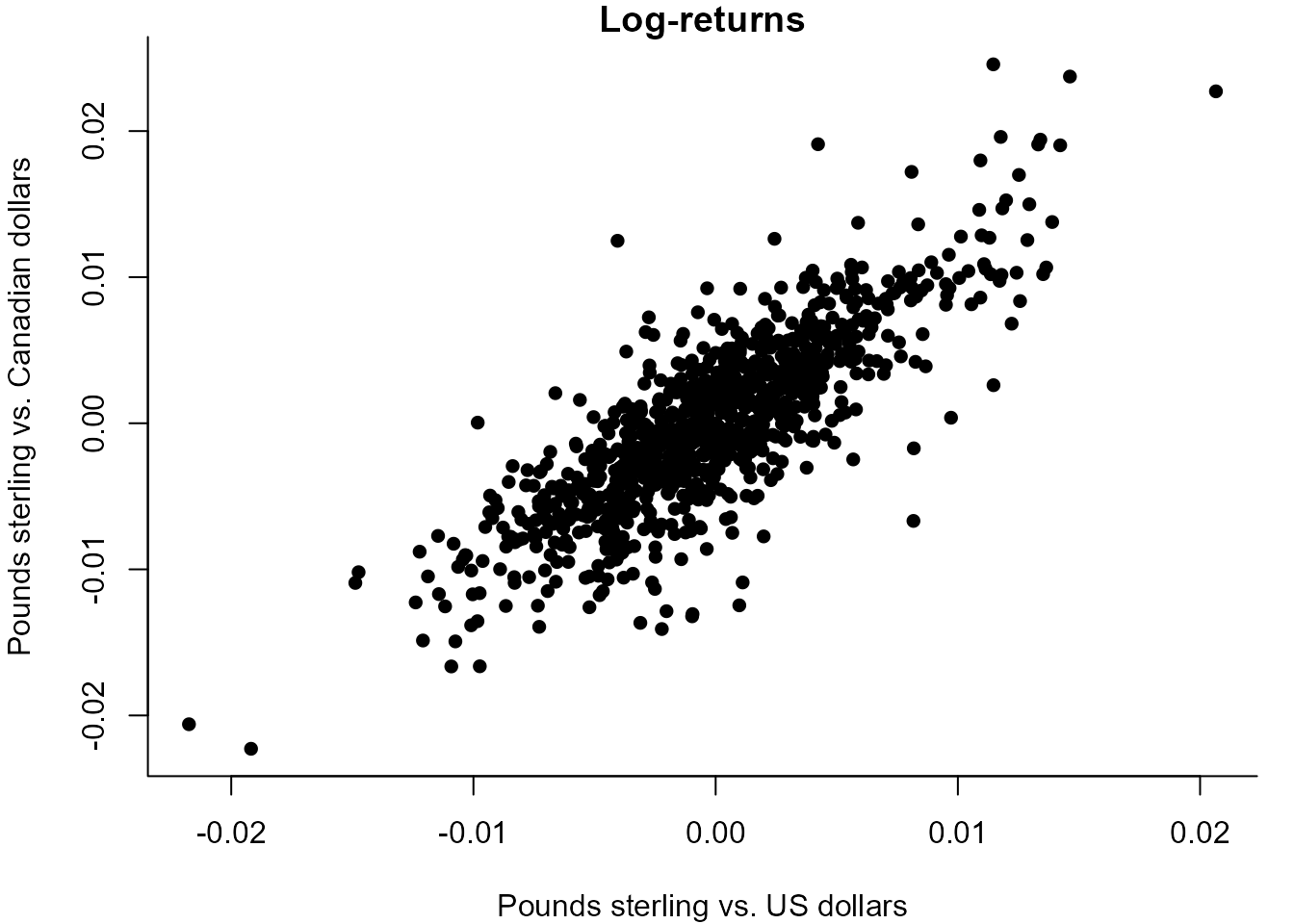

The R function cor

R provides a function cor to calculate sample correlation coefficients. By default, it calculates the sample (product moment) correlation coefficient given in Section 10.2.1.

We can supply either two vectors x and y of equal length or a matrix with columns containing the vectors of data for which we want to calculate the sample correlation coefficient. In this case, we create a 2-column matrix using cbind function to combine the 2 vectors USDlogr and CADlogr columnwise into a matrix.

If we supply a matrix then R will return a matrix containing the sample correlation coefficients between all possible pairs of columns in the input matrix, including between each column and itself, which produces values of 1 on the diagonal of the output matrix. If we supply vectors x and y then it does not matter which vector is entered as x and which as y.

> cor(x = USDlogr, y = CADlogr)
[1] 0.8201113
> cor(x = CADlogr, y = USDlogr)
[1] 0.8201113
> cor(x = cbind(USDlogr, CADlogr))
          USDlogr   CADlogr
USDlogr 1.0000000 0.8201113
CADlogr 0.8201113 1.0000000

Anscombe’s Quartet of datasets

In Section 10.3.6 Anscombe’s Quartet of dataset are provided in Figure 10.9. These 4 datasets are available as separate data frames in the anscombiser package Northrop (2022). Use install.packages("anscombiser") to install this package.

> library(anscombiser)

> cor(anscombe1)
          x1        y1
x1 1.0000000 0.8164205
y1 0.8164205 1.0000000
> cor(anscombe2)
          x2        y2
x2 1.0000000 0.8162365
y2 0.8162365 1.0000000
> cor(anscombe3)
          x3        y3
x3 1.0000000 0.8162867
y3 0.8162867 1.0000000
> cor(anscombe4)
          x4        y4
x4 1.0000000 0.8165214
y4 0.8165214 1.0000000

We see that the paired data in these datasets have almost exactly the same sample correlation coefficient. They have many other summary statistics in common. See Section 10.3.6 for details.

The method argument to cor enables us to ask R to calculate Spearman’s rank correlation coefficient (See Section 2.3.5). The values of this sample correlation coefficient differ between these datasets.

> cor(anscombe1, method = "spearman")
          x1        y1
x1 1.0000000 0.8181818
y1 0.8181818 1.0000000
> cor(anscombe2, method = "spearman")
          x2        y2
x2 1.0000000 0.6909091
y2 0.6909091 1.0000000
> cor(anscombe3, method = "spearman")
          x3        y3
x3 1.0000000 0.9909091
y3 0.9909091 1.0000000
> cor(anscombe4, method = "spearman")
    x4  y4
x4 1.0 0.5
y4 0.5 1.0

References

Northrop, Paul J. 2022. anscombiser: Create Datasets with Identical Summary Statistics.