Chapter 3: Probability

Paul Northrop

This vignette provides R code to reproduce some of the content of Chapter 3 of the STAT0002 notes.

Kerrich’s coin data

A summary of these data are available in the data frame kerrich. Use ?kerrich for more information.

> library(stat0002)

> # This code produces the plot in Figure 3.1 of the STAT0002 notes
> plot(kerrich$throws, kerrich$heads / kerrich$throws,
+      ylab = "proportion of heads",
+      xlab = "number of throws (logarithmic scale)", lwd = 2, type = "l",
+      log = "x", ylim = c(0,1), axes = FALSE)
> abline(h = 0.5, lty = 2)
> axis(1, labels = as.character(c(3, 10, 30, 100, 300, 1000, 3000, 10000)),
+      at=c(3, 10, 30, 100, 300, 1000, 3000, 10000))
> axis(2, labels = c(0, 0.2, 0.4, 0.5, 0.6, 0.8, 1.0),
+      at=c(0, 0.2, 0.4, 0.5, 0.6, 0.8, 1.0))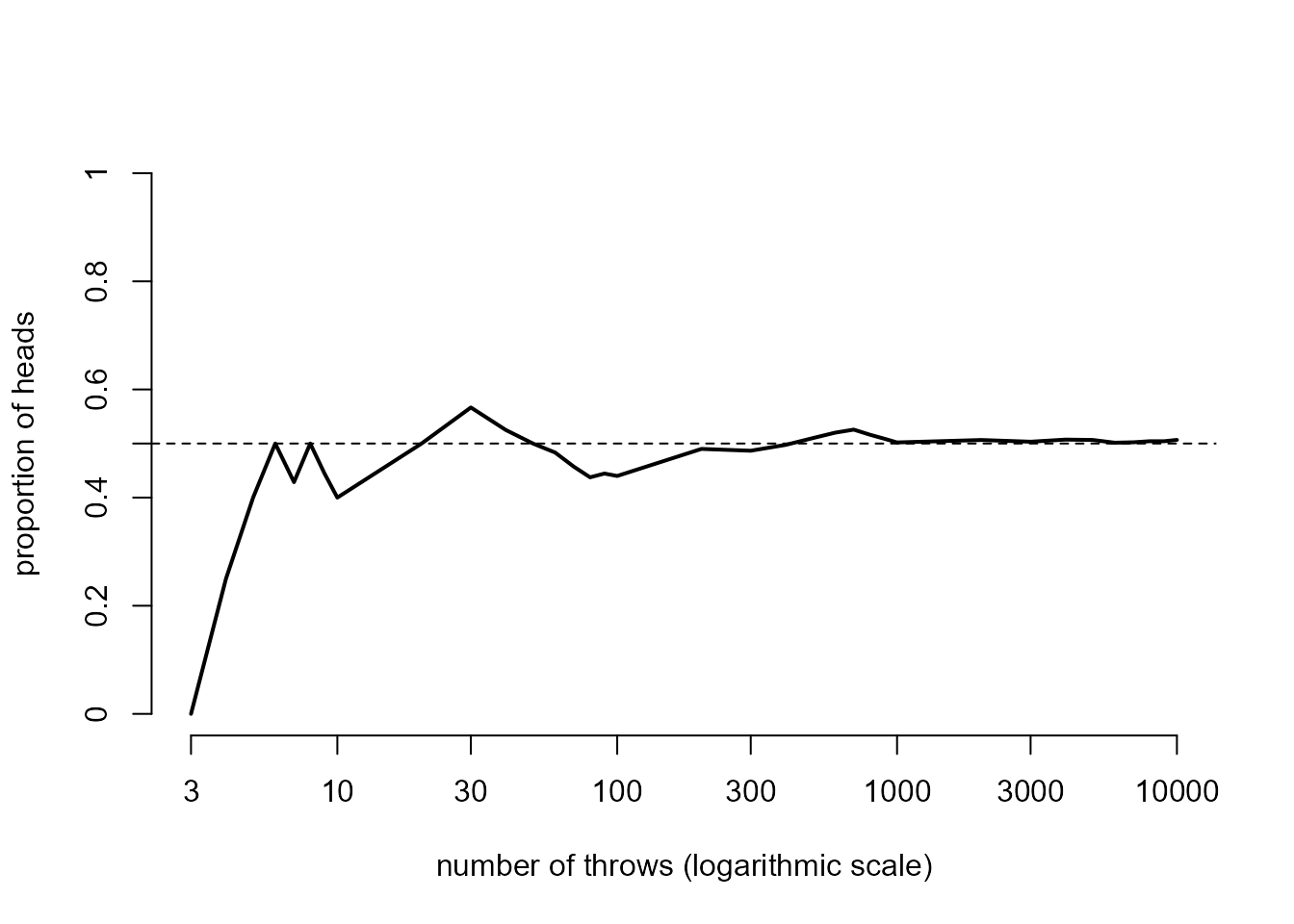

We could extract from the data frame kerrich the number of trials (the 10,000 throws of the coin) and the number of heads. From this we can calculate an estimate of the probability $P(H)$ that the outcome of a trial is a head.

> trials <- kerrich[nrow(kerrich), "throws"]
> heads <- kerrich[nrow(kerrich), "heads"]
> c(heads, trials)
[1]  5067 10000
> phat <- heads / trials
> phat
[1] 0.5067

Graduate Admissions at Berkeley

The object berkeley is a 3-dimensional array that contains information about applicants to graduate school at UC Berkeley in 1973 for the six largest departments. Use ?UCBAdmissions for more information. The 3 dimensions of the array correspond to the gender of the applicant (dimension named Gender), whether or not they were admitted (named Admit) and a letter code for the department to which they applied (named Dept). A given entry in berkeley gives the total number of applicants in the corresponding (Admit, Gender, Dept) category. In Chapter 3 we consider only the dimensions Admit and Gender.

The following code collapses the 3-dimensional array to a 2-dimensional array by summing the frequencies over all the six departments, which gives the central part of Table 3.3 in the notes.

> # 2-way table: sex and outcome
> sex_outcome <- apply(berkeley, 2:1, FUN = sum)
> colnames(sex_outcome) <- c("A", "R")
> rownames(sex_outcome) <- c("M", "F")
> sex_outcome
      Admit
Gender    A    R
     M 1198 1493
     F  557 1278

Now we add the column and row totals.

> # Add column totals
> sex_outcome <- rbind(sex_outcome, total = colSums(sex_outcome))
> # Add row totals
> sex_outcome <- cbind(sex_outcome, total = rowSums(sex_outcome))
> sex_outcome
         A    R total
M     1198 1493  2691
F      557 1278  1835
total 1755 2771  4526

We can divide by $n$ (4526) to produce Table 3.5 of the notes.

> # Convert frequencies to probabilities
> pso <- sex_outcome/ sex_outcome[3, 3]
> round(pso, 3)
          A     R total
M     0.265 0.330 0.595
F     0.123 0.282 0.405
total 0.388 0.612 1.000

Notice that sex_outcome[3, 3] extracts the [3, 3] element of the matrix sex_outcome, that is, 4526.

Can you use R to perform some of the calculations that are performed in Section 3.4 and/or 3.5 of the notes?

Blood types data

A summary of these data are available in the data frame blood_types.

> blood_types
  ABO  Rh percentage
1   O Rh+         37
2   A Rh+         35
3   B Rh+          8
4  AB Rh+          3
5   O Rh-          7
6   A Rh-          7
7   B Rh-          2
8  AB Rh-          1

One way to estimate the probabilities given on which Table 3.13 is based is to use the aggregate function.

> aggregate(percentage ~ Rh, data = blood_types, FUN = sum) 
   Rh percentage
1 Rh-         17
2 Rh+         83
> aggregate(percentage ~ ABO, data = blood_types, FUN = sum)
  ABO percentage
1   A         42
2  AB          4
3   B         10
4   O         44

To divide by 100 to convert the frequencies to estimates of probability we could do the following.

> propn <- function(x) sum(x) / 100
> aggregate(percentage ~ Rh, data = blood_types, FUN = propn) 
   Rh percentage
1 Rh-       0.17
2 Rh+       0.83
> aggregate(percentage ~ ABO, data = blood_types, FUN = propn)
  ABO percentage
1   A       0.42
2  AB       0.04
3   B       0.10
4   O       0.44