Chapter 9: Linear regression
Paul Northrop
Source:vignettes/stat0002-ch9-linear-regression-vignette.Rmd
stat0002-ch9-linear-regression-vignette.RmdThis vignette provides some R code that is related to some of the content of Chapter 9 of the STAT0002 notes, namely to (simple) linear regression.
Example data
We use the Hubble data described at the start of Section
9.1 of the notes. These data are available in the data frame
hubble.
> hubble
distance velocity
1 0.032 170
2 0.034 290
3 0.214 -130
4 0.263 -70
5 0.275 -185
6 0.275 -220
7 0.450 200
8 0.500 290
9 0.500 270
10 0.630 200
11 0.800 300
12 0.900 -30
13 0.900 650
14 0.900 150
15 0.900 500
16 1.000 920
17 1.100 450
18 1.100 500
19 1.400 500
20 1.700 960
21 2.000 500
22 2.000 850
23 2.000 800
24 2.000 1090
> plot(rev(hubble), pch = 16)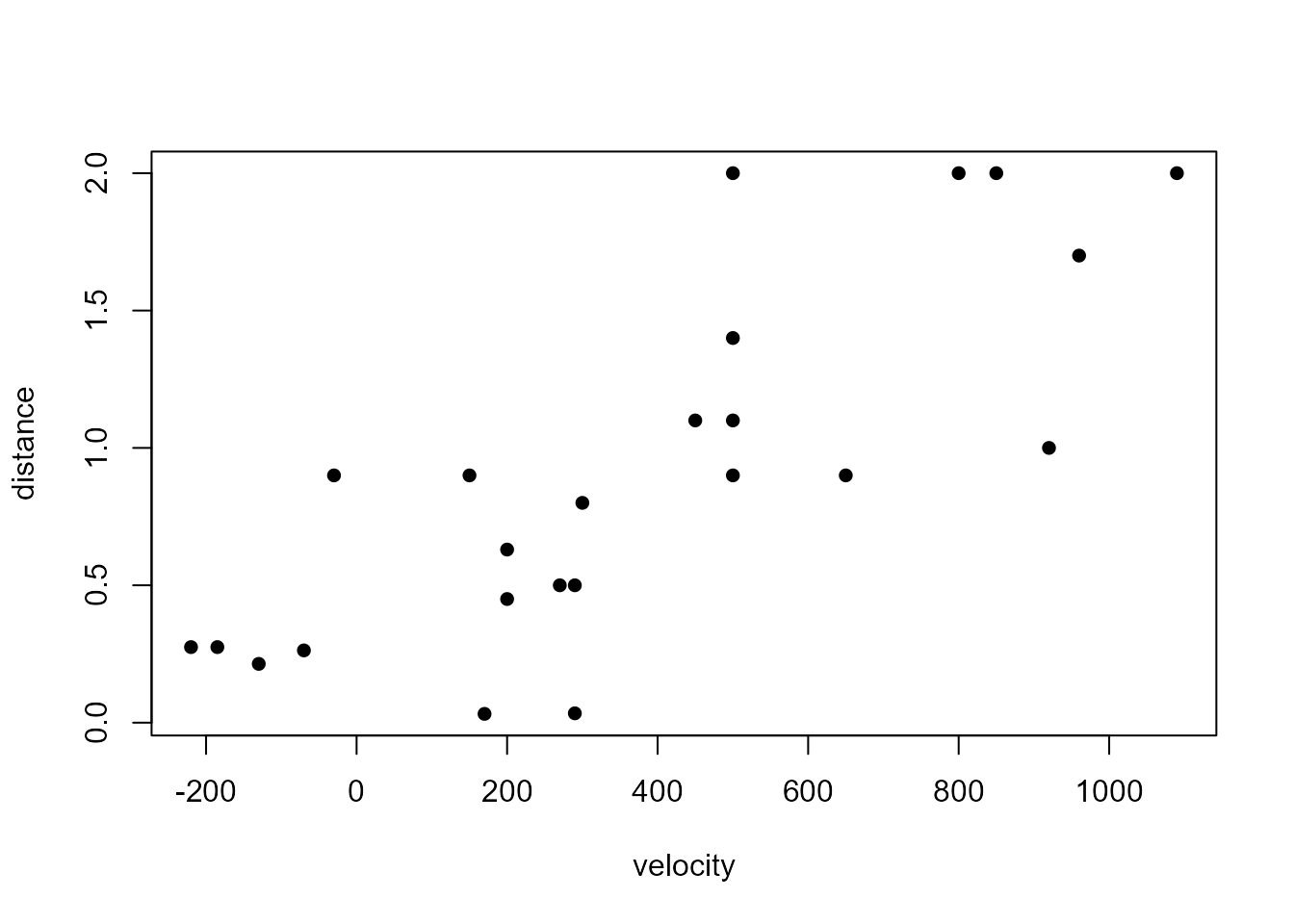
The R function lm
R provides a function lm to fit linear regression
models. The following code fits a simple linear regression model to the
hubble data, with distance as the response
variable and velocity as the one explanatory variable. The
lm function can do much more than this For example, it can
fit a regression model that has more one explanatory variable.
> l3 <- lm(distance ~ velocity, data = hubble)
> l3
Call:
lm(formula = distance ~ velocity, data = hubble)
Coefficients:
(Intercept) velocity
0.399098 0.001373
> coef(l3)
(Intercept) velocity
0.399098216 0.001372936 The point estimates of the intercept \(\alpha\) and gradient \(\beta\) regression parameters agree with
those in the title of Figure 9.6 of the notes. Note that
coef is a generic function that (tries to) extracts
parameter estimates from a fitted model object.
Our own function slm
As an exercise in writing an R function and to demonstrate that the
expressions for the least squares estimators \(\hat{\alpha}\) and \(\hat{\beta}\) given in Section
9.1.2 are correct, we write our own function slm to
perform simple linear regression. We give our returned (list) object the
class "lm", including the call (the code that
calls the function slm) and the coefficients
(estimated of the regression parameters \(\alpha\) and \(\beta\)) so that when we print our results
they looks like those from lm. We also include other useful
quantities, with names that should indicate what they contain.
We include an argument rto, which stands for “regression
through the origin”. For these data, Hubble’s Law gives us a reason to
consider a special linear regression model in which the fitted line is
forced to go through the origin, that is, the intercept parameter \(\alpha\) is set to \(0\) rather than being estimated from the
data. We also deal with the situation where no explanatory data are
provided. For further information see Section
9.1.3 of the notes.
> slm <- function(y, x, rto = FALSE) {
+ # If only response data are provided then fit a horizontal line y = mean(y)
+ if (missing(x)) {
+ residuals <- y - mean(y)
+ rss <- sum(residuals ^ 2)
+ n <- length(y)
+ estimates <- mean(y)
+ names(estimates) <- "(Intercept)"
+ res <- list(coefficients = estimates, fitted.values = mean(y),
+ residuals = y - mean(y), rss = rss,
+ sigmahat = sqrt(rss / (n - 1)), y = y, call = match.call())
+ class(res) <- "lm"
+ return(res)
+ }
+ # Check that y and x have the same length
+ if (length(y) != length(x)) {
+ stop("''y'' and ''x'' must have the same length")
+ }
+ # Calculate the estimates. If rto = FALSE (the default) then we estimate
+ # both alpha and beta from the data. If rto = TRUE then we set alpha = 0
+ # and estimate only beta from the data.
+ ybar <- mean(y)
+ if (rto) {
+ betahat <- mean(x * y) / mean(x ^ 2)
+ alphahat <- 0
+ estimates <- betahat
+ names(estimates) <- deparse(substitute(x))
+ } else {
+ xbar <- mean(x)
+ betahat <- mean((x - xbar) * (y - ybar)) / mean((x - xbar) ^ 2)
+ alphahat <- ybar - betahat * xbar
+ estimates <- c(alphahat, betahat)
+ names(estimates) <- c("(Intercept)", deparse(substitute(x)))
+ }
+ # Calculate the fitted values for y, residuals and residual sum of squares
+ fittedy <- alphahat + betahat * x
+ residuals <- y - fittedy
+ rss <- sum(residuals ^ 2)
+ # Estimate of the error standard deviation sigma
+ n <- length(y)
+ p <- length(estimates)
+ sigmahat <- sqrt(rss / (n - p))
+ # Create the results list
+ res <- list(coefficients = estimates, fitted.values = fittedy,
+ residuals = residuals, rss = rss, sigmahat = sigmahat,
+ y = y, x = x, call = match.call())
+ class(res) <- "lm"
+ return(res)
+ }The following code fits Model 3 from Section 9.1.3, plots the data again and adds the fitted regression line.
> # Model 3
> m3 <- slm(y = hubble$distance, x = hubble$velocity)
> m3
Call:
slm(y = hubble$distance, x = hubble$velocity)
Coefficients:
(Intercept) hubble$velocity
0.399098 0.001373
> plot(rev(hubble), pch = 16)
> abline(coef = coef(m3))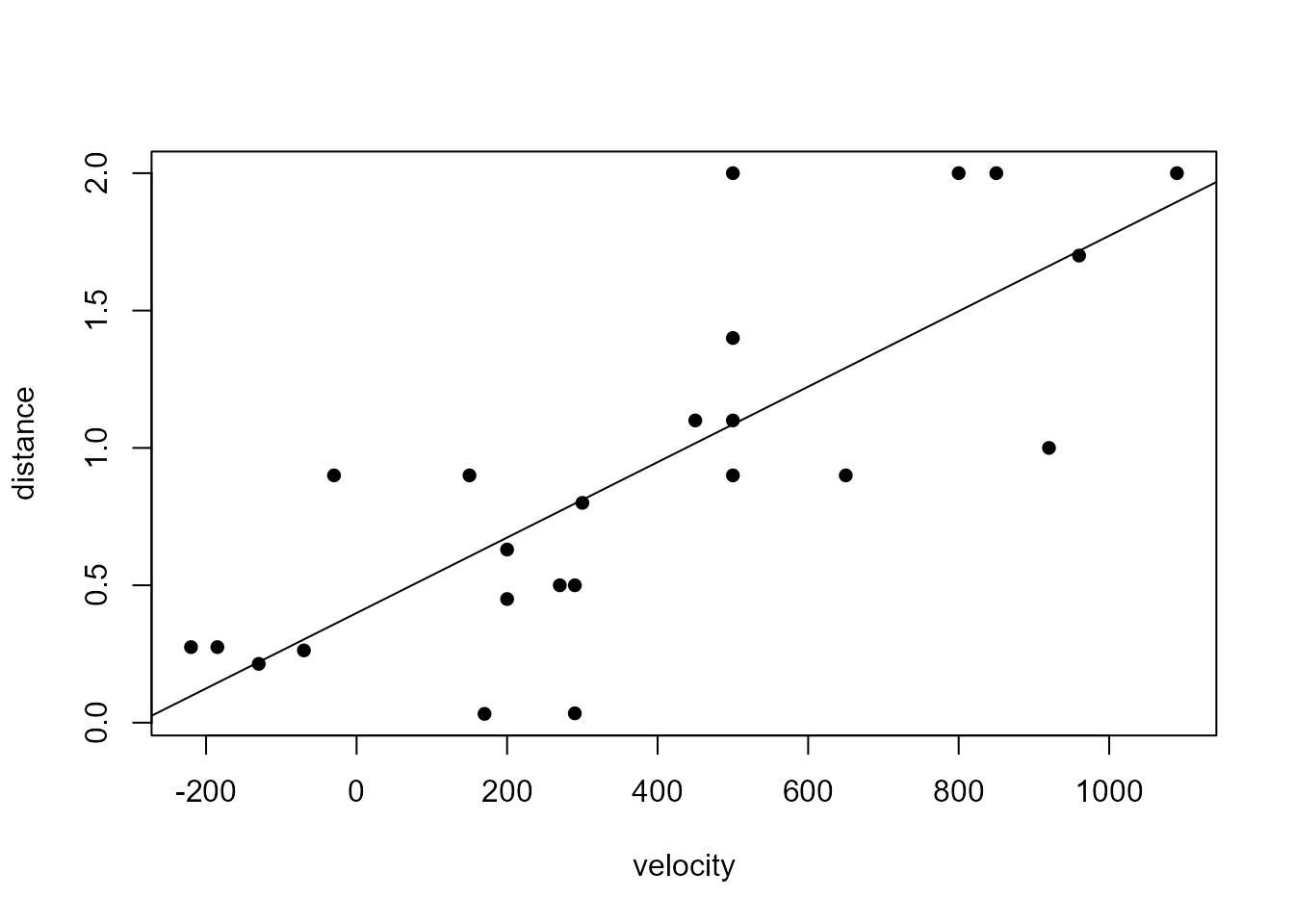
For the sake of completeness we also fit Models 1 and 2 from Section
9.1.3, which assume, respectively, that \(\beta=0\) and that \(\alpha = 0\), and show that our results
agree with those from lm.
> # Model 1
> # ~1 means that there is no explanatory variable in the model
> m1 <- slm(y = hubble$distance)
> l1 <- lm(distance ~ 1, data = hubble)
> coef(m1)
(Intercept)
0.911375
> coef(l1)
(Intercept)
0.911375
>
> # Model 2
> # The -1 removes the intercept from the model
> m2 <- slm(y = hubble$distance, x = hubble$velocity, rto = TRUE)
> l2 <- lm(distance ~ velocity - 1, data = hubble)
> coef(m2)
hubble$velocity
0.001921806
> coef(l2)
velocity
0.001921806 Estimating the error standard deviation
An unbiased estimator of the error variance \(\sigma^2\) is the sum of the squared
residuals divided by \(n - p\), where
\(n\) is the sample size and \(p\) is the number of parameter estimated.
See Section
9.1.2, which considers the case where both \(\alpha\) and \(\beta\) are estimated. In the following,
sigma is a function that (tries to) calculate an estimate
of the standard deviation \(\sigma\) of
the errors. It does this, as is commonly the case, by taking by square
root of the estimate of \(\sigma^2\).
Again, our function agrees with the output from lm.
Standardised residuals
In Section 9.3 of the notes we define the standardised residuals for the \(i\)th observation in the data by
\[r_i^S = \frac{r_i}{\hat{\sigma}(1-h_{ii})},\]
where \(r_i\) is the residual for
observation \(i\), \(\hat{\sigma}\) is the estimate of the error
standard deviation and \[h_{ii} = \frac1n +
\frac{(x_i - \bar{x}) ^ 2}{\sum_{i=1}^n (x_i - \bar{x}) ^ 2}.\]
is the leverage of observation \(i\). If the model is correct then these
residuals have approximately a variance of 1. If the errors are normally
distributed then these residuals should look like a sample from a
standard normal distribution. We write a function to calculate these
standardised residuals for a model fit produced by slm and
use this function in the next section to produce a normal QQ plot of
standardised residuals.
> stres <- function(slmfit) {
+ # The generic function nobs tries to calculate the number of observations
+ n <- nobs(slmfit)
+ # Extract the values of the explanatory variables
+ x <- slmfit$x
+ # Calculate the leverage value for each observation
+ sx2 <- (x - mean(x)) ^ 2
+ hii <- 1 / n + sx2 / sum(sx2)
+ return(slmfit$residuals / (slmfit$sigmahat * sqrt(1 - hii ^ 2)))
+ }Residual plots
We plot the residuals against the values of the explanatory variable, velocity, and then against the fitted values. When there is only one explanatory variable these plots will look identical, apart from a change of scale on the horizontal axis. This is because each fitted values is a linear function, \(\hat{\alpha} + \hat{\beta} x\), of the corresponding value \(x\) of the explanatory variable.
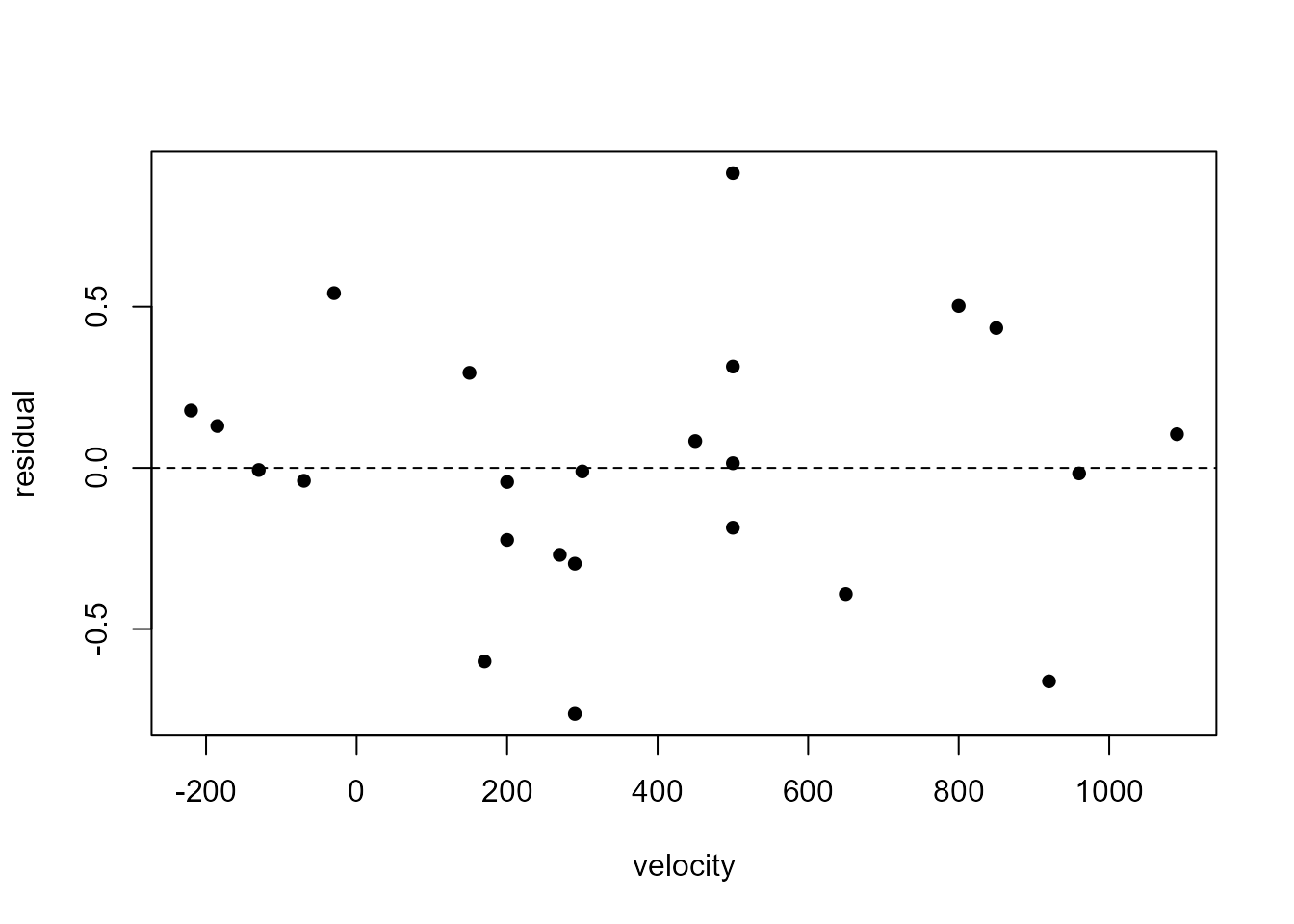
> plot(m3$fitted.values, m3$residual, ylab = "residual", xlab = "fitted values", pch = 16)
> abline(h = 0, lty = 2)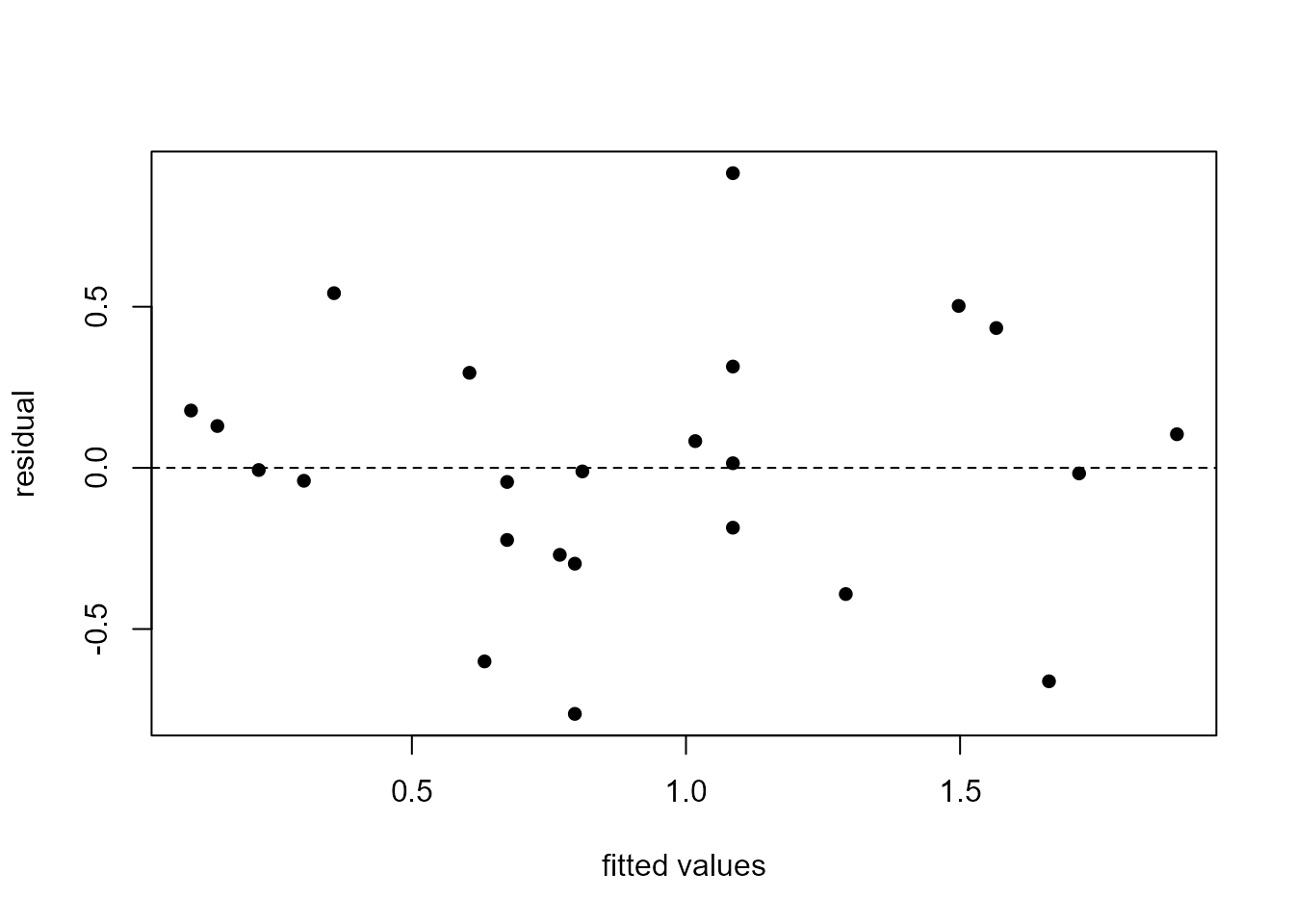
Now, we produce a normal QQ plot of the standardised residuals and
check that we is correct using the built-in plot function
for lm objects, selecting which = 2 to ask for
a normal QQ plot.
> stresiduals <- stres(m3)
> qqnorm(stresiduals, ylab = "Standardised Residuals")
> qqline(stresiduals)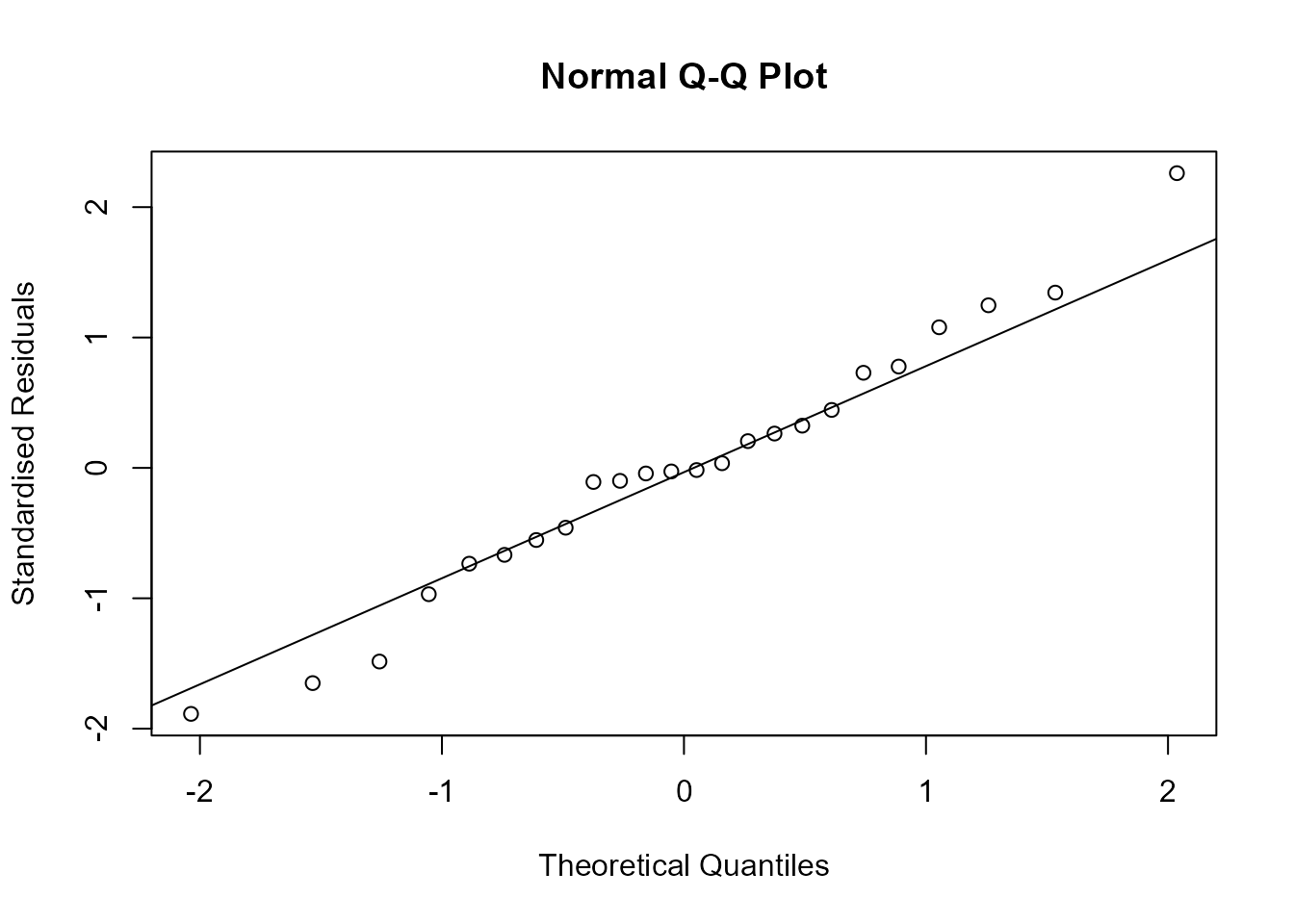
> # By default, the 3 residuals with the largest magnitudes are labelled by their observation number
> plot(l3, which = 2)