Normal sampling distributions movie
Source:R/normal_sampling_distribution_movie.R
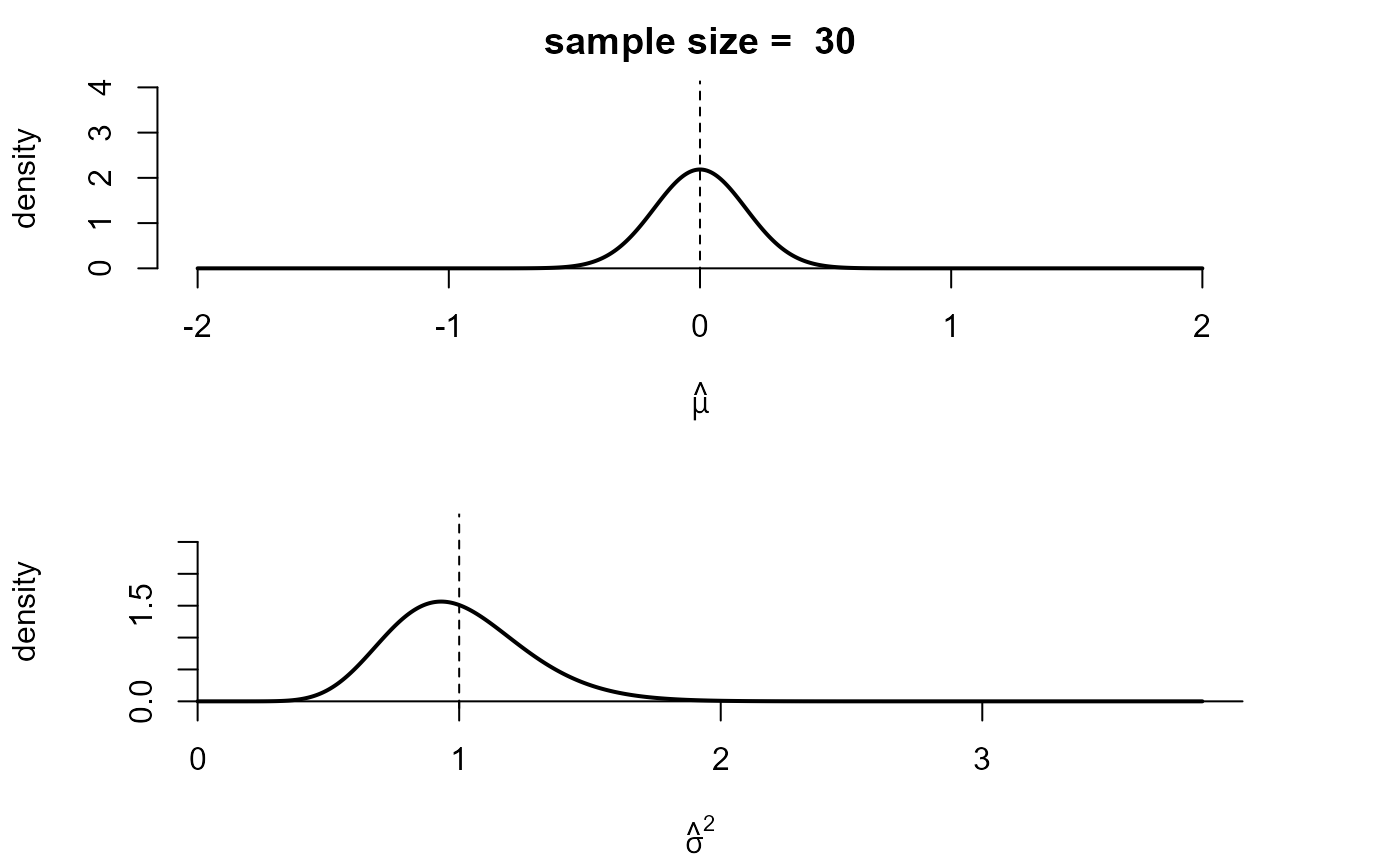
normal_sampling_distns_movie.RdA movie to show how the sampling distributions of the sample mean and sample variance based on a random sample from a normal distribution depend on the size \(n\) of the sample.
normal_sampling_distns_movie(starting_n = 30, delta_n = 1, mu = 0, sigma = 1)Arguments
- starting_n
A numeric scalar. The value of the sample size used to produce the first plot of the p.d.f.
- delta_n
A numeric scalar. The amount by which the value of the sample size is increased/decreased after one click of the +/- button.
- mu
A numeric scalar. The mean of the normal distribution from which the random sample are drawn.
- sigma
A numeric scalar. The standard deviation of the normal distribution from which the random sample are drawn.
Value
Nothing is returned, only the animation is produced.
Details
The movie is based on two plots. The top plot shows the
probability density function (p.d.f.) of the sampling distribution of the
sample mean, that is, a N(\(\mu\), \(\sigma\)^2 / n) distribution.
The bottom plot contains the p.d.f. of the sampling distribution of the
sample variance, that is, a gamma distribution
(GammaDist) with shape parameter
\((n - 1) / 2\) and rate parameter \((n - 1) / 2\sigma^2\).
The number of samples simulated is increased
The value of the sample size can be changed using the +/- buttons in the panel. For the purposes of this movie the value of \(n\) cannot exceed 100.
See also
stat0002movies: general information about the movies.
Examples
normal_sampling_distns_movie()
