Exponential Quantile-Quantile plots

Source: R/graphs.R

Produces a QQ plot to compare ordered sample data to corresponding quantiles of an exponential distribution fitted to these data.

qqexp(
  y,
  statistic = c("mean", "median"),
  type = 6,
  envelopes = FALSE,
  ...,
  line = list(col = "black", lty = 1, lwd = 1)
)

Arguments

y

Sample data

statistic

A character scalar. Selects the summary statistic used to estimate \(\lambda\), either the sample mean or sample median.

type

An integer scalar. If statistic = "median" then this is passed to quantile to select the type of sample quantile used to estimate the sample median. The default, type = 6, selects the estimator defined in the STAT002 notes.

envelopes

Determines whether or not simulation envelopes should be added to the plot. If envelopes = FALSE then no envelopes are added. If envelopes is a positive integer (a common choice is 19) then simulation envelopes based on this many simulated datasets are added. The limits of of the envelopes are indicated using short horizontal lines.

...

Optional arguments to be passed to plot such as xlab, ylab, main and/or graphical parameters such as pch, lty and lwd, to control the appearance of the main plot. To change the appearance of the line of equality use the argument line.

line

Determines whether or not a line of equality is superimposed on the plot. If a line is required then must be a list, which can contain graphical parameters passed to abline, such as col, lty and lwd to control the appearance of the line. If line is not a list, for example, line = 0, then no line is superimposed.

Value

The estimate of \(\lambda\).

Details

The rate parameter \(\lambda\) of the exponential distribution is estimated using 1/mean(y, na.rm = TRUE) if statistic = "mean" and log(2)/quantile(y, probs = 0.5, na.rm = TRUE) if statistic = "median". The ordered sample data are plotted against quantiles of this fitted exponential distribution. Specifically, the \(i\)th smallest sample observation is plotted against the \(100 i / (n + 1)\%\) theoretical exponential quantile, where \(n\) is the sample size. The plot is constrained to be square. A line of equality is superimposed on the plot.

See also

qqnorm to produce a normal QQ plot.

Examples

## Australian Birth Times Data

# Calculate the waiting times until each birth
waits <- diff(c(0, aussie_births[, "time"]))

# Estimating lambda using the sample mean
qqexp(waits)

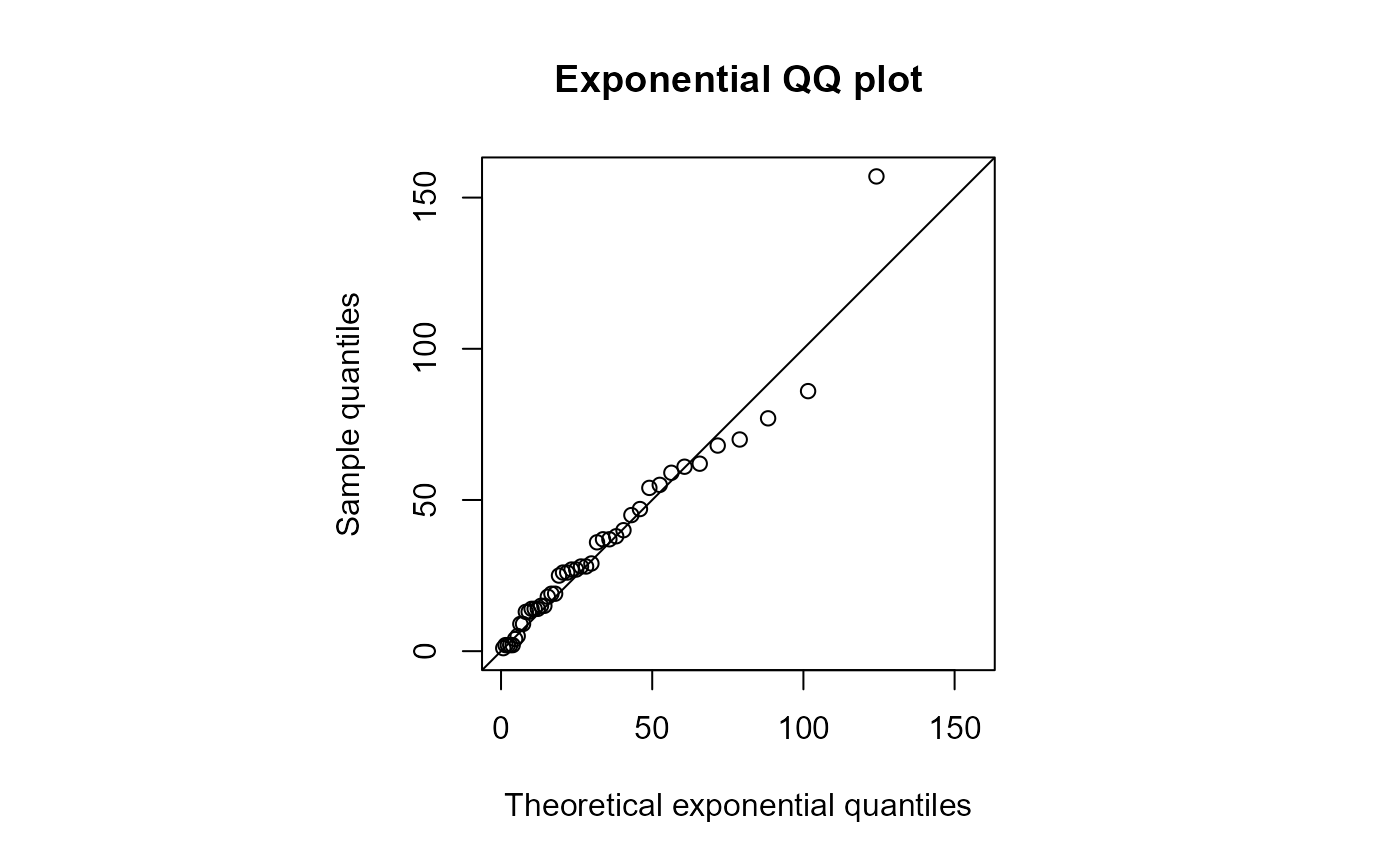#> estimate of lambda 
#>         0.03066202 

# Change the appearance of the points and line
qqexp(waits, pch = 16, line = list(lty = 2, col = "blue", lwd = 2))

#> estimate of lambda 
#>         0.03066202 

# Add simulation envelopes
qqexp(waits, envelopes = 19)

#> estimate of lambda 
#>         0.03066202 

# Estimating lambda using the sample median
qqexp(waits, statistic = "median", envelopes = 19)

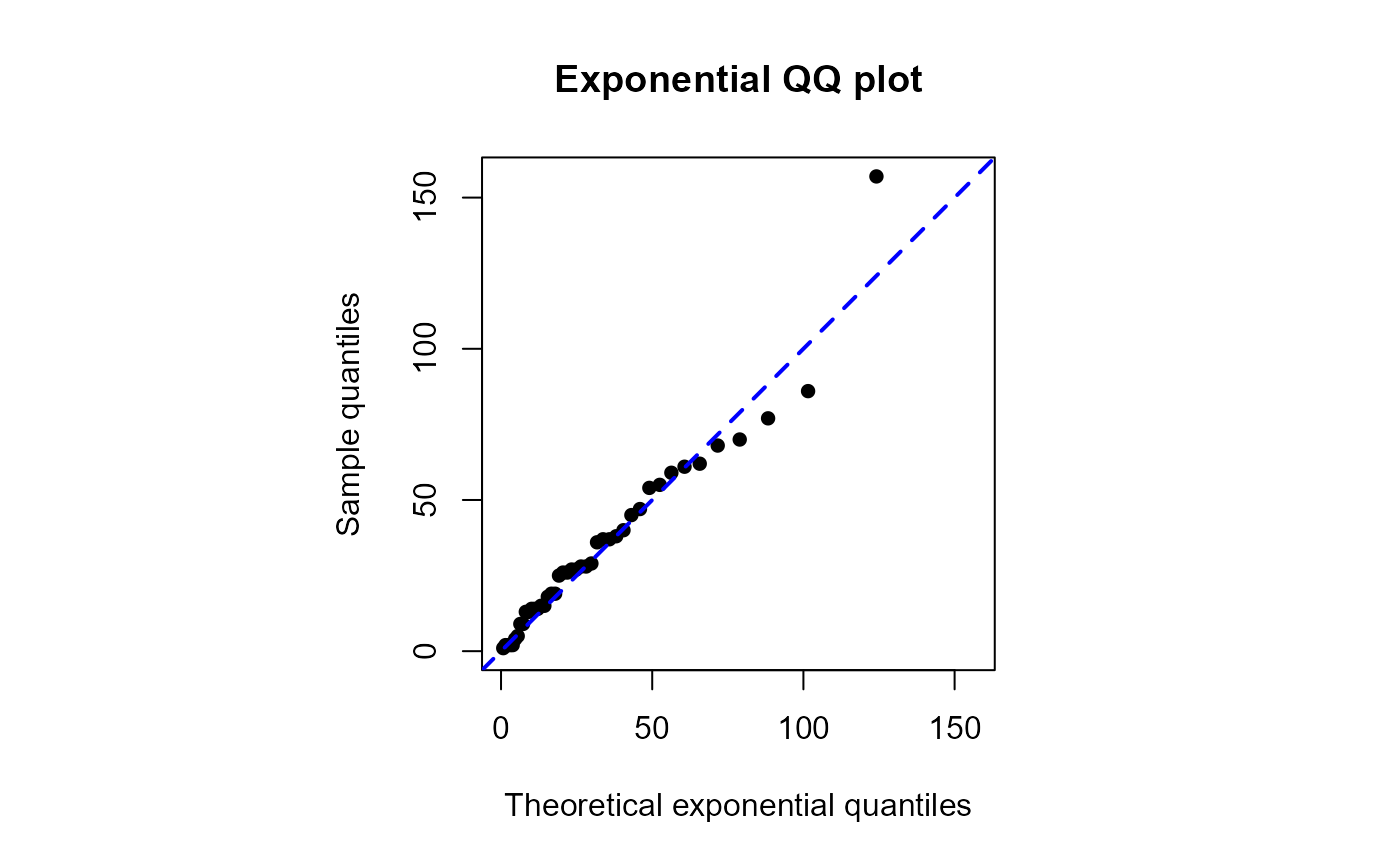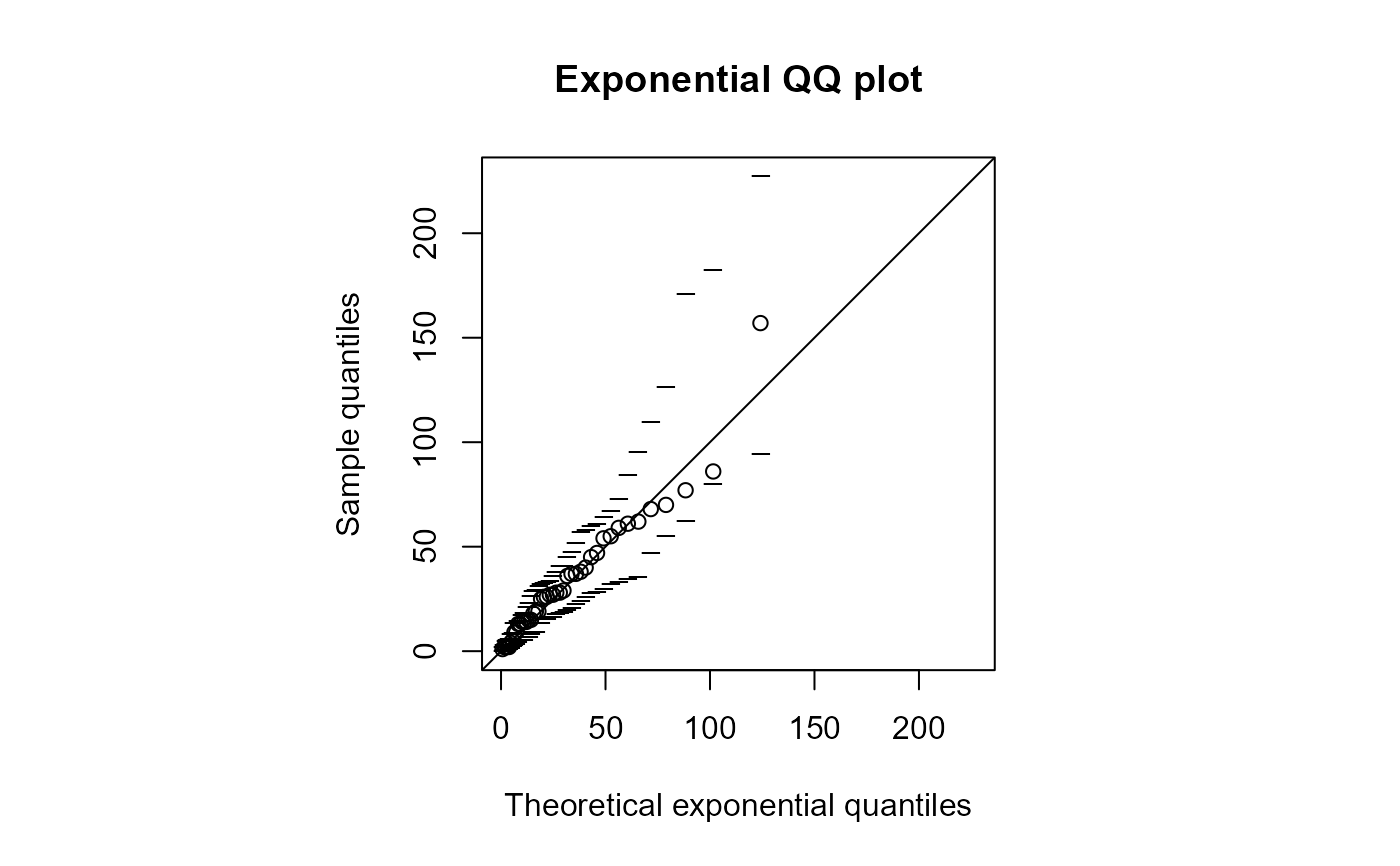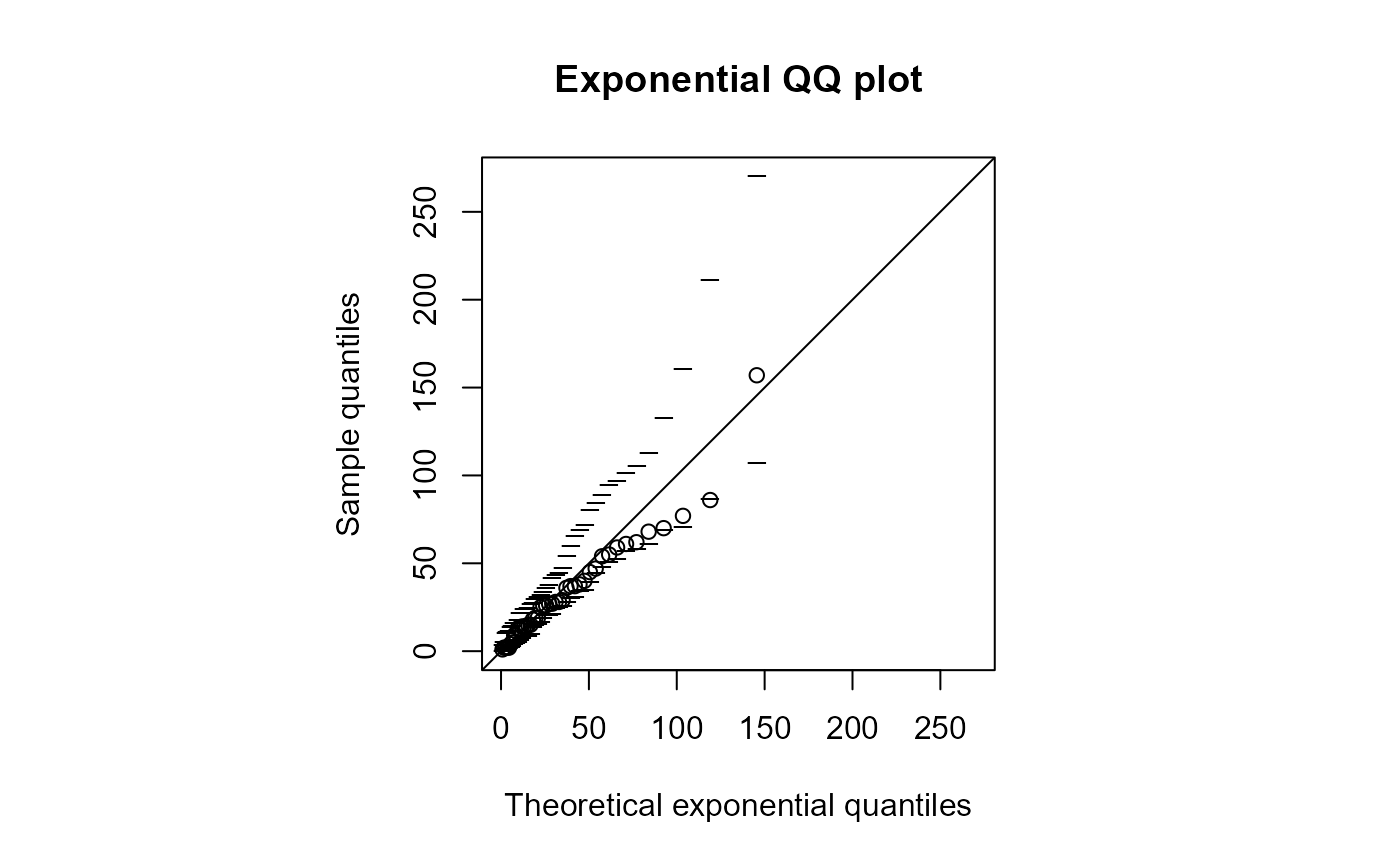#> estimate of lambda 
#>          0.0261565